Элементы комбинаторики. Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики

Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего методы решения комбинаторных задач – т.е. задач, связанных с подсчетом числа различных комбинаций.

Пусть A₁, A₂, …, A_k – элементы конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.

Правило суммы. Если элемент А₁ может быть выбран n₁ способами, элемент А₂ – n₂ способами, …, элемент А_k – n_k способами, то выбор одного из элементов (или А₁, или А₂, …, или A_k) может быть осуществлен n₁ + n₂ + … + n_k способами.

Пример 1.3. В группе 30 студентов. Известно, что 5 из них на экзамене по математике получили оценку «отлично», 10 – оценку «хорошо», остальные – «удовлетворительно». Сколько существует способов выбрать одного студента, получившего на экзамене оценку «отлично» или «хорошо»?

Решение. Студент, получивший оценку «отлично» может быть выбран n₁ = 5 способами, оценку «хорошо» – n₂ = 10 способами. По правилу суммы существует n₁ + n₂ = 5 + 10 = 15 способов выбора одного студента, получившего на экзамене оценку «отлично» или «хорошо». ◄

Правило произведения. Если элемент А₁ может быть выбран n₁ способами, после этого элемент А₂ может быть выбран n₂ способами, …, после каждого такого выбора элемент А_k может быть выбран n_k способами, то выбор всех элементов А₁, А₂, …, A_k в указанном порядке может быть осуществлен n₁·n₂·…·n_k способами.

Пример 1.4. В группе 30 студентов. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 30 студентов, его заместителем – любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n₁=30, n₂=29, n₃ = 28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно n₁·n₂·n₃ = 30·29·28 = = 24360 способов. ◄

Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из m элементов (0 ≤ m ≤n). Например, из 5 элементов a, b, c, d, e могут быть отобраны комбинации по 2 элемента – ab, bc, cd, ba и т.д., по 3 элемента – abc, cbd, cba и т.д.

Если комбинации из n элементов по m отличаются либо составом элементов, либо порядком их расположения (либо и тем и другим), то такие комбинации называют размещениями из n элементов по m.

Число размещений из n элементов по m находится по формуле

,

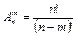(1.5)

где n! равно произведению n первых чисел натурального ряда, т.е. n! = 1·2·…·n.

Пример 1.5. Сколько можно записать двузначных чисел, используя без повторения цифры от 1 до 5?

Решение. В данном случае двузначное число является комбинацией из пяти цифр по две цифры. Поскольку числа отличаются как составом входящих в них цифр, так и порядком их расположения, то в данном случае двузначные числа являются размещениями из пяти цифр по две. Число таких размещений

. ◄

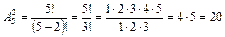Если комбинации из n элементов по m отличаются только составом элементов (порядок их расположения не имеет значения), то такие комбинации называют сочетаниями из n элементов по m.

Число сочетаний из n элементов по m находится по формуле

.

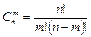(1.6)

Пример 1.6. Необходимо выбрать в подарок две из пяти имеющихся различных книг. Сколькими способами можно это сделать?

Решение. Из смысла задачи следует, что порядок выбора книг не имеет значения. Здесь важен только их состав. Поэтому в данном случае комбинации книг представляют собой сочетания из 5 книг по 2. Число таких комбинаций

. ◄

Если в размещениях из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения называют размещениями с повторениямииз n элементов по m. Число размещений с повторениями равно

,

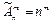(1.7)

Пример 1.7. Сколько можно записать трехзначных чисел, которые не содержат цифр 0 и 5?

Решение. В данном случае трехзначное число является комбинацией из восьми цифр (0 и 5 не учитываются) по три цифры. При этом некоторые из цифр (или все) могут повторяться. Поэтому в данном случае трехзначные числа является размещениями с повторениями из восьми цифр по три. Число таких размещений с повторениями

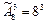= 512. ◄

Если в сочетаниях из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие сочетания называют сочетаниями с повторениями из n элементов по m.

Число сочетаний с повторениями равно

,

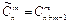(1.8)

где 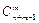определяется по формуле (1.6).

Пример 1.8. В почтовом отделении продаются открытки восьми видов. Сколькими способами можно купить в нем три открытки?

Решение. Учитывая, что порядок выбора открыток не имеет значения, а важен только их состав, причем некоторые из открыток (или все) могут оказаться одинаковыми, искомое число способов находим по формуле числа сочетаний с повторениями

= 120. ◄

Если комбинации из n элементов отличаются только порядком расположения элементов, то такие комбинации называют перестановкамииз n элементов. Число перестановок из n элементов находится по формуле

Пример 1.9. Порядок выступления 5 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 5 элементов. Их число равно P₅ = 5! = 1·2·3·4·5 = 120. ◄

Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется n₁ раз, 2-й элемент – n₂ раз, k-й элемент – n_k раз, причем n₁ + n₂ + … + n_k = n, то такие перестановки называют перестановками с повторениями из n элементов. Число перестановок с повторениями равно

.

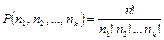(1.10)

Пример 1.10. Сколько можно составить шестизначных чисел, состоящих из цифр 3, 5, 7, в которых цифра 3 повторяется 3 раза, цифра 5 – 2 раза, цифра 7 – 1 раз?

Решение. Каждое шестизначное число отличается от другого порядком следования цифр (причем n₁ =3, n₂ = 2, n₃ = 1, а их сумма равна 6), т.е. является перестановкой с повторениями из 6 элементов. Их число равно

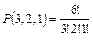= 60. ◄

АЛГЕБРА СОБЫТИЙ

Ранее мы познакомились со способами непосредственного вычисления вероятностей простых событий. Однако на практике чаще приходится иметь дело со сложными событиями, которые являются комбинацией простых событий. Для нахождения вероятностей таких событий применяются теоремы сложения и умножения вероятностей. Перед тем, как сформулировать эти теоремы введем понятия суммы событий и произведения событий.