Классическое и статистическое определение вероятности
Для практической деятельности необходимо уметь сравнивать события по степени возможности их наступления. Рассмотрим классический случай. В урне находится 10 шаров, 8 из них белого цвета, 2 черного. Очевидно, что событие «из урны будет извлечен шар белого цвета» и событие «из урны будет извлечен шар черного цвета» обладают разной степенью возможности их наступления. Поэтому для сравнения событий нужна определенная количественная мера.
Количественной мерой возможности наступления события является вероятность. Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Классическое определение вероятности связано с понятием благоприятствующего исхода. Остановимся на этом подробнее.
Пусть исходы некоторого испытания образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Такие исходы называют элементарными исходами, или случаями. При этом говорят, что испытание сводится к схеме случаев или «схеме урн», т.к. любую вероятностную задачу для подобного испытания можно заменить эквивалентной задачей с урнами и шарами разных цветов.
Исход называется благоприятствующим событию А, если появление этого случая влечет за собой появление события А.
Согласно классическому определению вероятность события А равна отношению числа исходов, благоприятствующих этому событию, к общему числу исходов, т.е.
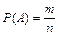 , ,
| (1.1) |
где Р(А) – вероятность события А; m – число случаев благоприятствующих событию А; n – общее число случаев.
Пример 1.1. При бросании игральной кости возможны шесть исходов – выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления четного числа очков?
Решение. Все n = 6 исходов образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Событию А – «появление четного числа очков» – благоприятствуют 3 исхода (случая) – выпадение 2, 4 или 6 очков. По классической формуле вероятности события получаем
Р(А) = 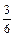 =
= 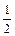 . ◄
. ◄
Исходя из классического определения вероятности события, отметим ее свойства:
1. Вероятность любого события заключена между нулем и единицей, т.е.
0 ≤ Р(А) ≤ 1.
2. Вероятность достоверного события равна единице.
3. Вероятность невозможного события равна нулю.
Как было сказано ранее, классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытаний, обладающих симметрией возможных исходов, т.е. сводящихся к схеме случаев. Однако существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения.
Например, если допустить, что монета сплющена, то очевидно, что события «появление герба» и «появление решки» нельзя считать равновозможными. Поэтому формула для определения вероятности по классической схеме в данном случае неприменима.
Однако существует другой подход при оценке вероятности событий, основанный на том, насколько часто будет появляться данное событие в произведенных испытаниях. В этом случае используется статистическое определениевероятности.
Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.
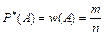 , ,
| (1.2) |
где Р*(А) – статистическая вероятность события А; w(A) – относительная частота события А; m – число испытаний, в которых появилось событие А; n – общее число испытаний.
В отличие от математической вероятности Р(А), рассматриваемой в классическом определении, статистическая вероятность Р*(А) является характеристикой опытной, экспериментальной. Иначе говоря, статистической вероятностью события А называется число, относительно которого стабилизируется (устанавливается) относительная частота w(А) при неограниченном увеличении числа испытаний, проводимых при одном и том же комплексе условий.
Например, когда про стрелка говорят, что он попадает в цель с вероятностью 0,95, то это означает, что из сотни выстрелов, произведенных им при определенных условиях (одна и та же цель на том же расстоянии, та же винтовка и т.д.), в среднем бывает примерно 95 удачных. Естественно, не в каждой сотне будет 95 удачных выстрелов, иногда их будет меньше, иногда больше, но в среднем при многократном повторении стрельбы в тех же условиях этот процент попаданий будет оставаться неизменным. Цифра 0,95, служащая показателем мастерства стрелка, обычно очень устойчива, т.е. процент попаданий в большинстве стрельб будет для данного стрелка почти один и тот же, лишь в редких случаях отклоняясь сколько-нибудь значительно от своего среднего значения.
Еще одним недостатком классического определения вероятности (1.1), ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания. В некоторых случаях этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).
Пусть плоская фигура g составляет часть плоской фигуры G (рис. 1.1). На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении попадания на нее брошенной случайной точки. Полагая, что вероятность события А – попадания брошенной точки на фигуру g – пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, найдем
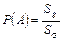 , ,
| (1.3) |
где Sg и SG – соответственно площади областей g и G.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок), двумерной (плоская фигура) или трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е.
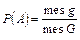 . .
| (1.4) |

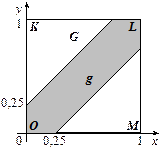
Рис. 1.1 Рис 1.2
Пример 1.2. Два студента условились встретиться в определенном месте между 10 и 11 часами дня. Пришедший первым ждет второго в течение 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода между 10 и 11 часами.
Решение. Обозначим моменты прихода в определенное место первого и второго студентов соответственно через x и y. В прямоугольной системе координат Oxy возьмем за начало отсчета 10 часов, а за единицу измерения – 1 час. По условию 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1 (рис. 1.2). Событие А – встреча двух студентов – произойдет, если разность между x и не y превзойдет 1/4 часа (по абсолютной величине), т.е. |y – x| ≤ 0,25.
Решение этого неравенства есть полоса x – 0,25 ≤ y ≤ x + 0,25, которая внутри квадрата G представляет заштрихованную область g. По формуле (1.3)
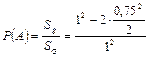 = 0,4375.◄
= 0,4375.◄
Дата добавления: 2015-11-10; просмотров: 10159;
