Вероятнейшее число появлений события при повторении испытаний.
Задача 3. Садовод сделал осенью 6 прививок. По опыту прошлых лет известно, что после зимовки 7 из каждых 10 черенков оставались жизнеспособными. Какое число прижившихся черенков наиболее вероятно?
Решение. Будем условно считать, что вероятность события, состоящего в том, что привитый черенок приживется, одинакова для всех черенков и равна 0,7 и что испытания независимы.
Составим следующую таблицу, учитывая, что p = 0,7, g = 0,3.
Таблица 1.1
| Вероятности | Число прижившихся черенков | |||||||
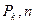
| 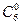 ∙0,36× ×0,70 ∙0,36× ×0,70
| 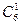 ∙0,7× ×0,35 ∙0,7× ×0,35
| 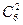 ∙0,72× ×0,34 ∙0,72× ×0,34
| 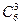 ∙0,73× ×0,33 ∙0,73× ×0,33
| 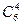 ∙0,74× ×0,32 ∙0,74× ×0,32
| 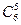 ∙0,75× ×0,3 ∙0,75× ×0,3
| 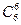 ∙0,76× ×0,30 ∙0,76× ×0,30
| |
| 0,0007 | 0,0102 | 0,0593 | 0,1852 | 0,3241 | 0,3025 | 0,1176 |
Из таблицы видно, что наибольшая вероятность соответствует событию, состоящему в том, что приживутся 4 черенка. Следовательно, это событие более возможно, чем все остальные.
Решим задачу в общем виде, не составляя приведенную выше таблицу.
Обозначим число появлений события А, имеющего наибольшую вероятность при п испытаниях, через k0. Тогда
Рk0,n ≥ Рk0+1,n (1.8.2)
и
Рk0,n ≥ Рk0+1,n (1.8.3)
Из (1.8.2) имеем
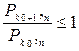
или, учитывая формулу Бернулли (1.8.1),
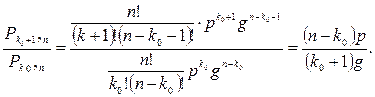 (1.8.4)
(1.8.4)
Из последнего неравенства следует, что
(n – k0) p ≤ (k0 + 1) g
После перегруппировки получаем
np – g ≤ k0 (p + g),
откуда имеем
np – g ≤ k0 (1.8.5)
Запишем следствие из неравенства (1.8.3)
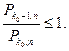
Выполняя те же преобразования, что и для (1.8.2), имеем
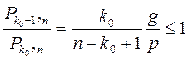
или
k0 (g + p) ≤ np + p
откуда окончательно получаем
k0 ≤ np + p (1.8.6)
Объединяя (1.8.5) и (1.8.6), имеем
np–g≤k0≤np+p. (1.8.7)
Числа np–g и np+p отличаются на единицу. Поэтому, если np–g-дробное число, то nр+р - также дробное и неравенство (1.8.7) определяет одно k0. Если np–g- целое число, то и nр+р - также целое; тогда числа k0 и k0+1 будут иметь равную и наибольшую вероятность.
В задаче о садоводе вычислим k0. Имеем n = 6, p = 0,7, g = 0,3; np–g = 6∙0,7–0,3 = 3,9; np+p = 6∙0,7 + 0,7 = 4,9; 3,9≤k0≤4,9; k0 = 4.
Дата добавления: 2015-09-21; просмотров: 1633;
