ФОРМУЛА БЕРНУЛЛИ

Задача 1. Допустим, что на опытной делянке посеяно 15 семян. Примем, что всхожесть всех семян одинакова и равна 80%. Возможны следующие элементарные события:

А₀ = {число семян, давших росток, равно 0};

А₁ = {число взошедших семян равно 1};

А₂ = {число взошедших семян равно 2};

и т. д. и, наконец,

A₁₅ = {все семена дадут всходы}.

Как найти вероятности этих событий, в частности, вычислить вероятность того, что из 15 посеянных семян взойдет ровно 12, безразлично в какой последовательности?

Рассмотрим серию из n независимых испытаний, в каждом из которых некоторое событие А имеет одну и ту же вероятность Р(А) = р, не зависящую от номера испытания.

Такая серия испытаний называется схемой Бернулли.

Решим следующую задачу. В условиях схемы Бернулли определим вероятность P_k,n события, состоящего в том, что при п повторениях испытания событие А, которое имеет одну и ту же вероятность появления в каждом испытании, произойдет ровно k раз безразлично в какой последовательности. Элементарными исходами испытаний являются:

событие 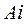= {появление события А в i-м испытании} (i = l, 2, 3, ..., n), P(A_i) = p;

событие 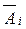= {непоявление события А в i-м испытании} (i=1, 2, 3,..., п), P( 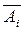)=1 – p = g.

Предположим, что событие А имело место в k первых испытаниях и не произошло в п–k последующих, т. е. в соответствии с определением произведения событий, произошло событие A₁A₂A₃...A_k 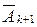...A_n. Так как испытания независимы, то, применив теорему умножения вероятностей, получим

.

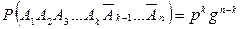Число способов наступления сложного события, состоящего в появлении события А именно k раз и непоявлении n – k раз равно числу всевозможных множеств, которые можно образовать из п элементов по k элементов, и отличающихся только составом. Число таких множеств

равно 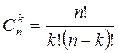[см. формулу (1.2.3)].

Итак, вероятность наступления события А ровно k раз в серии n - испытаний равно

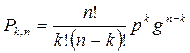(1.8.1)

Это формула Бернулли. Здесь п – число повторений независимых испытаний; k – число испытаний, в которых событие А произошло (число успехов); р – вероятность появления события А в одном испытании; g - вероятность непоявления события А в одном испытании (g = 1–p); P_k,n – вероятность сложного события, состоящего в том, что при п испытаниях событие А наступило ровно k раз.

Вернемся к сформулированной выше задаче.

1. Число посеянных семян равно числу независимых испытаний, т. е. n = 15,число «успехов» k= 12, p = 0,8, g = 1 – 0,8 = 0,2. Тогда

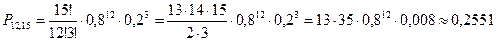
Событие «12 из 15» имеет небольшую вероятность. Если наблюдать такие серии повторений испытаний, то 12 успехов из 15 испытаний будут иметь место в среднем в 25 сериях из 100.