МУАВРА-ЛАПЛАСА

Задача. На опытном поле посеяно 1500 семян. Найти вероятность события, состоящего в том, что всходы дадут ровно 1200 семян, если условно считать, что каждое зерно взойдет с вероятностью 0,9.

По формуле (11.8.2), учитывая, что п = 1500, k = 1200, р = 0,9, g = 0,l, находим

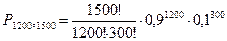
Получение ответа сопряжено с немалыми вычислительными трудностями. Ясно, что при большом числе п повторений испытаний вычисление вероятностей по формуле Бернулли становится громоздким.

Приближенная формула для частного случая p = ¹/₂ впервые была доказана Муавром в 1730г., а впоследствии Лаплас привел обобщенную формулу для 0 <р < 1.

Теорема. Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р (0<р<1), то справедлива следующая формула:

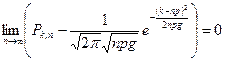(1.9.1)

где P_k,_n - вероятность того, что при n испытаниях событие А появится ровно k раз (k испытаний успешны) ; g = 1–р- вероятность непоявления со бытия А в одном испытании. Для практических целей используют приближенное равенство - следствие из формулы (1.9.1):

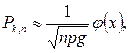(1.9.2)

где 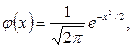а x=

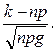
Формула (1.9.2) дает тем более точный результат, чем больше число n.

Для функции j(х) составлены таблицы. Так как j (х) зависит от x в четной степени, то j (x) = j (–х). Поэтому таблицы составлены для значений x≥0 (см. Приложение 1).

Пример. Вернемся к исходной задаче и найдем P_1200,1500 по формуле (1.9.2). При n=1500, k=1200, p = 0,9, g = 0,1 имеем

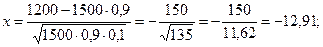
j(-12,91) = j(12,91)»6,3∙10^–4;

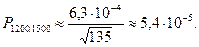
Как видим, вероятность мала. Событие, состоящее в том, что из посеянных 1500 семян взойдет ровно 1200, при одной серии испытаний, практически не произойдет.

Интегральная теорема Муавра - Лапласа. Если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна р (0<р<1), то справедлива формула

,

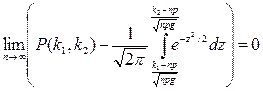где P(k₁, k₂) - вероятность того, что при n повторениях испытания событие А имеет место не менее чем k₁ и не более k₂ раз. При решении задач применяют следствие из теоремы:

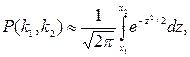(1.9.3)

где

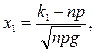
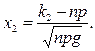(1.9.4)

Интеграл 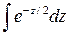не выражается через элементарные функции. Для вычисления вероятностей по формуле (1.9.3) используют хорошо изученную функцию

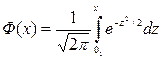
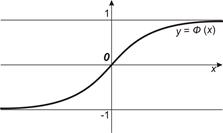Рис. 1

Для нее составлены таблицы, а график изображен на рис. 1. Функцию Ф(x) часто называют функцией Лапласа. Функция Ф(х) нечетная, Ф(x) = –Ф(–х), так что таблицы составлены только для х≥0.

В окончательном виде вероятность:

P(k₁,k₂) » Ф(x2) – Ф(x1). (1.9.6)

Пример. В лаборатории из партии семян, имеющих всхожесть 90%, высеяно 600 семян Найти вероятность события = {число семян, давших всходы, не менее 520 и не более 570}, если принять, что каждое посеянное зерно взойдет с одной и той же вероятностью Р = 0,9

Решение. Имеем n = 600, p = 0,9, g = 0,1, следовательно,

P(520,570) » Ф(x₂) – Ф(x₁),

где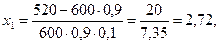

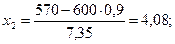
P(520,570) » Ф(4,08) – Ф(–2,72) = 0,49996 + 0,4967 = 0,99.

Событие практически достоверное.