Теорема сложения вероятностей для случая, когда события совместны.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, минус вероятность их совместного появления, т. е.

P(A+B)=P(A)+P(B)–P(AB) (1.6.8)

По определению событие А+В состоит в наступлении или события 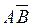, или события 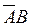, или события АВ, следовательно,

.

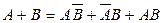События, стоящие в правой части равенства, несовместны: появление одного из них исключает появление остальных. Поэтому

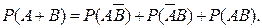(1.6.9)

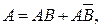
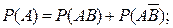
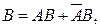
Но 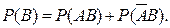Следовательно,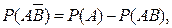 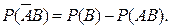Подставим эти значения в (1.6.9). Имеем

P(A+B)=P(A)+P(B)–P(AB). (1.6.10)

Пример 2. В посевах пшеницы на делянке имеется 95% здоровых растений. Выбирают два растения. Определить вероятность того, что среди них хотя бы одно окажется здоровым.

Пусть события А₁ = {первое растение здоровое}; событие А₂ = {второе растение здоровое}; событие А₁+А₂ = {хотя бы одно растение здоровое}. Так как события А₁ и А₂ совместны, то

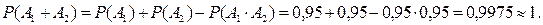
Событие А₁+А₂ практически достоверно. Задачу можно решить и другим способом. При повторных испытаниях, как это имело место в задаче, появление хотя бы одного события (А₁ + А₂) и непоявление события ни разу ( 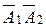) - события противоположные; тогда

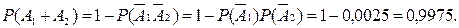
Как мы видим, получен один и тот же результат.