П. 1.6. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ
Определение. Суммой или объединением двух событий A и B называется событие C, состоящее в появлении хотя бы одного из них.
Обозначают C = A + B, или C =  , или C =(A или B).
, или C =(A или B).
Пример. Пусть A - событие, состоящее в том, что наудачу выбранная из стада корова имеет годовой удой от 3000 до 3500 кг, B - событие, состоящее в том, что выбранная корова имела удой свыше 3500 кг. Тогда событие C=A+B означает, что выбранная корова имеет удой свыше 3000 кг.
Нахождение вероятности наступления суммы двух событий основывается на следующей теореме.
1. Теорема сложения вероятностей. Вероятность наступления одного из двух несовместных событий равна сумме их вероятностей, т. е.
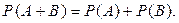 (1.6.1)
(1.6.1)
Доказательство. Пусть n - число всех возможных элементарных событий, при которых может наступить событие A или событие B. Пусть mA - число равновозможных элементарных событий, благоприятных для A, mB - такое же число для события B. Имеем

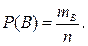
Очевидно, mА + mВ-число элементарных событий, благоприятных для появления события или A, или B, так что
P(A или B)=P(A+B)= 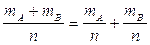 =P(A)+P(B).
=P(A)+P(B).
Теорема доказана.
Теорема сложения для большего числа попарно несовместных событий формулируется и доказывается аналогично:
 P (A или, B или C) = P(A+B+C)=P(A)+P(B)+P(C). (1.6.2)
P (A или, B или C) = P(A+B+C)=P(A)+P(B)+P(C). (1.6.2)
Следствие 1. Если события A, B, C образуют полную группу, то сумма их вероятностей равна 1.
Действительно, в результате испытания обязательно произойдет из этих событий (или B, или A, или C). Поэтому A + B + C - событие достоверное и
P(A+B+C)=1. (1.6.3)
Из (11.6.3) и (11.6.2) следует, что
P(A)+P(B)+P(C)=1.
Следствие 2. Сумма вероятностей двух противоположных событий A и 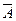 равна 1.
равна 1.
Противоположные события являются частным случаем событий, образующих полную группу, поэтому
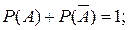 (1.6.4)
(1.6.4)
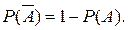 (1.6.5)
(1.6.5)
В частности, если вероятность попадания в мишень при одном выстреле равна 0,8, то вероятность промаха равна 1–0,8 = 0,2.
Пример. В ящике 4 белых, 5 красных, 8 зеленых и 3 голубых шара. Шары перемешивают и извлекают 1 шар. Какова вероятность события, состоящего в том, что шар окажется цветным?
Решение. Элементарными исходами являются события A = {извлечение белого шара}, B = {извлечение красного шара}, C - {извлечение зеленого шара}, D - {извлечение голубого шара}.
Интересующее нас событие состоит в появлении события B, или C, или D, т.е. события B+C+D. Так как события B, C, D - несовместны, то

Дата добавления: 2015-09-21; просмотров: 979;
