Интегральная теорема Лапласа
Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе испытаний n приближенно равна
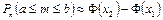 , ,
| (3.5) |
| где | 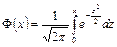 – –
| (3.6) |
функция (или интеграл вероятностей) Лапласа;
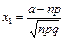 ; ; 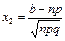 . .
| (3.7) |
Интегральная формула Лапласа, также как и локальная формула Муавра-Лапласа, тем точнее, чем больше n и чем ближе к 0,5 значения p и q. Вычисление по этой формуле дает незначительную погрешность при выполнении условия npq ≥ 20, хотя допустимым можно считать выполнение условия npq > 10.
Функция Ф(x) табулирована (см. Приложение 2). Для применения этой таблицы нужно знать свойства функции Ф(x):
1. Функция Ф(x) – нечетная, т.е. Ф(–x) = – Ф(x).
2. Функция Ф(x) – монотонно возрастающая, причем при x → +∞ Ф(x) → 0,5 (практически можно считать, что уже при x ≥ 5 Ф(x) ≈ 0,5).
Пример 3.4. По условиям примера 3.3 вычислить вероятность того, что от 300 до 360 (включительно) студентов успешно сдадут экзамен с первого раза.
Решение. Применяем интегральную теорему Лапласа (npq ≥ 20). Вычисляем:
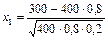 = –2,5;
= –2,5; 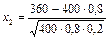 = 5,0;
= 5,0;
P400(300 ≤ m ≤ 360) = Ф(5,0) – Ф(–2,5).
Учитывая свойства функции Ф(x) и пользуясь таблицей ее значений, находим: Ф(5,0) = 0,5; Ф(–2,5) = – Ф(2,5) = – 0,4938.
Получаем P400(300 ≤ m ≤ 360) = 0,5 – (– 0,4938) = 0,9938. ◄
Запишем следствия интегральной теоремы Лапласа.
Следствие 1. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что число m наступления события А отличается от произведения np не более, чем на величину ε > 0 (по абсолютной величине) равна
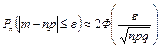 . .
| (3.8) |
Пример 3.5. По условиям примера 3.3 найти вероятность того, что от 280 до 360 студентов успешно сдадут экзамен по теории вероятностей с первого раза.
Решение. Вычислить вероятность Р400(280 ≤ m ≤ 360) можно аналогично предыдущему примеру по основной интегральной формуле Лапласа. Но проще это сделать, если заметить, что границы интервала 280 и 360 симметричны относительно величины np =320. Тогда на основании следствия 1 получаем
 =
= 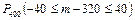 =
= 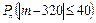 ≈
≈
≈ 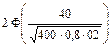 = 2Ф(5,0) ≈ 2·0,5 ≈ 1,
= 2Ф(5,0) ≈ 2·0,5 ≈ 1,
т.е. практически достоверно, что от 280 до 360 студентов успешно сдадут экзамен с первого раза. ◄
Следствие 2. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что частость m/n события А заключена в пределах от α до β (включительно) равна
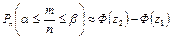 , ,
| (3.9) |
| где | 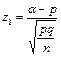 , ,  . .
| (3.10) |
Пример 3.6. По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет заключена в пределах от 0,9 до 0,95.
Решение. Вероятность того, что новорожденный доживет до 50 лет равна р = 0,87. Так как n = 1000 велико (т.е. условие npq = 1000·0,87·0,13 = 113,1 ≥ 20 выполнено), то используем следствие 2 интегральной теоремы Лапласа. Находим:
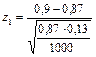 = 2,82,
= 2,82, 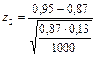 = 7,52.
= 7,52.
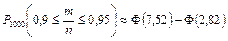 = 0,5 – 0,4976 = 0,0024. ◄
= 0,5 – 0,4976 = 0,0024. ◄
Следствие 3. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что частость m/n события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине) равна
 . .
| (3.11) |
Пример 3.7. По условиям предыдущей задачи найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине).
Решение. Используя следствие 3 интегральной теоремы Лапласа, находим:
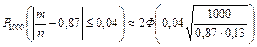 = 2Ф(3,76) = 2·0,4999 = 0,9998.
= 2Ф(3,76) = 2·0,4999 = 0,9998.
Так как неравенство 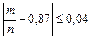 равносильно неравенству
равносильно неравенству 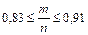 , полученный результат означает, что практически достоверно, что от 83 до 91% новорожденных из 1000 доживут до 50 лет. ◄
, полученный результат означает, что практически достоверно, что от 83 до 91% новорожденных из 1000 доживут до 50 лет. ◄
Ранее мы установили, что для независимых испытаний вероятность числа m появлений события А в n испытания находится по формуле Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р ≤ 0,1). В этом случае (n велико, р мало) применяют теорему Пуассона
Формула Пуассона
Теорема. Если вероятность p наступления события А в каждом испытании стремится к нулю (p → 0) при неограниченном увеличении числа n испытаний (n→ ∞), причем произведение np стремится к постоянному числу λ (np → λ), то вероятность Pn(m) того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству
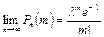 . .
| (3.12) |
Строго говоря, условие теоремы Пуассона (p → 0 при n → ∞, так что np → λ) противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании p = const. Однако, если вероятность p – постоянна и мала, число испытаний n – велико и число λ = np – незначительно (будем полагать, что λ = np ≤ 10), то из предельного равенства вытекает приближенная формула Пуассона
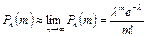 . .
| (3.13) |
Пример 3.8. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?
Решение. Вероятность того, что день рождения студента приходится на 1 сентября, равна р = 1/365. Так как вероятность р = 1/365 – мала, а число испытаний n = 1825 – велико и λ = np = 1825·(1/365) = 5 ≤ 10, то условие применимости формулы Пуассона выполняется. По формуле (3.13) получаем:
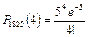 = 0,1755. ◄
= 0,1755. ◄
4. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Дата добавления: 2015-11-10; просмотров: 3233;
