Функция распределения случайной величины
Мы установили, что ряд распределения полностью характеризует дискретную случайную величину. Однако эта характеристика не является универсальной. Она существует только для дискретных величин. Для непрерывной величины ряд распределения построить нельзя. Действительно, непрерывная случайная величина имеет бесчисленное множество возможных значений, которые сплошь заполняют некоторый промежуток. Составить таблицу, в которой были бы перечислены все возможные значения этой величины, невозможно. Следовательно, для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он существует для дискретной величины. Однако различные области возможных значений случайной величины не являются одинаково вероятными, и для непрерывной величины все-таки существует «распределение вероятностей», хотя и не в том смысле, как для дискретной.
Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события Р(Х = х), состоящего в том, что случайная величина примет определенное значение х, а вероятностью события Р(Х <х), состоящего в том, что случайная величина примет значение меньшее х. Очевидно, что вероятность этого события зависит от х, т.е. является некоторой функцией от х.
Определение. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х:
| F(x) = P(X < x). | (4.2) |
Функцию распределения называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
 Функция распределения допускает простую геометрическую интерпретацию. Рассмотрим случайную величину Х на оси Ох (рис. 4.2), которая в результате опыта может занять то или иное положение. Пусть на оси выбрана точка, имеющая значение х. Тогда в результате опыта случайная величина Х может оказаться левее или правее точки х. Очевидно, вероятность того, что случайная величина Х окажется левее точки х, будет зависеть от положения точки х, т.е. являться функцией аргумента х.
Функция распределения допускает простую геометрическую интерпретацию. Рассмотрим случайную величину Х на оси Ох (рис. 4.2), которая в результате опыта может занять то или иное положение. Пусть на оси выбрана точка, имеющая значение х. Тогда в результате опыта случайная величина Х может оказаться левее или правее точки х. Очевидно, вероятность того, что случайная величина Х окажется левее точки х, будет зависеть от положения точки х, т.е. являться функцией аргумента х.
Для дискретной случайной величины Х, которая может принимать значения х1, х2, …, хn, функция распределения имеет вид
 , ,
| (4.3) |
где неравенство xi < х под знаком суммы означает, что суммирование касается всех тех значений xi, величина которых меньше х.
Пример 4.2. Дан ряд распределения случайной величины Х.
| xi | |||
| pi | 0,08 | 0,44 | 0,48 |
Найти и изобразить графически ее функцию распределения.
Решение. Будем задавать различные значения х и находить для них F(x) = = P(X < x).
1. Если х ≤ 0, то F(x) = P(Х < х) = 0.
2. Если 0 < х ≤ 1, то F(x) = P(Х < х) = P(Х = 0) = 0,08.
3. Если 1 < х ≤ 2, то F(x) = P(Х < х) = P(Х = 0) + P(Х = 1) = 0,08 + 0,44 = 0,52.
4. Если х > 2, то F(x) = P(Х < х) = P(Х = 0) + P(Х = 1) + P(Х = 2) = 0,08 + 0,44 + + 0,48 = 1.
Запишем функцию распределения.

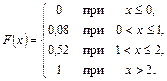
Изобразим функцию распределения графически (рис. 4.3). Заметим, что при подходе слева к точкам разрыва функция сохраняет свое значение (про такую функцию говорят, что она непрерывна слева). Эти точки на графике выделены. ◄
Этот пример позволяет прийти к утверждению, что функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.
Рассмотрим общие свойства функции распределения.
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
| 0 ≤ F(x) ≤ 1. | (4.4) |
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е.
| при х2 > х1 F(x1) ≥ F(x2). | (4.5) |
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т.е.
 , , 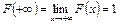 . .
| (4.6) |
4. Вероятность попадания случайной величины в интервал [х1, х2), включая х1, равна приращению ее функции распределения на этом интервале, т.е.
| P(х1 ≤ X < х2) = F(х2) – F(х1). | (4.7) |
Пример 4.3. Функция распределения случайной величины Х имеет вид:
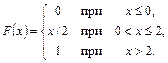
Найти вероятность того, что случайная величина X примет значение в интервале [1; 3).
Решение. P(1 ≤ X < 3) = F(3) – F(1) = 1 – 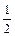 =
= 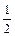 . ◄
. ◄
Для непрерывных случайных величин справедливо следующее свойство: Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.
Поясним это свойство. До сих пор мы рассматривали испытания, сводившиеся к схеме случаев, и нулевой вероятностью обладали лишь невозможные события. Из приведенного свойства следует, что нулевой вероятностью могут обладать и возможные события. На первый взгляд этот вывод может показаться парадоксальным. Действительно, если, например, событие α ≤ Х ≤ β имеет отличную от нуля вероятность, то оказывается, что оно представляет собой сумму событий, состоящих в принятии случайной величиной Х любых конкретных значений на отрезке [α, β] и имеющих нулевую вероятность.
Однако представления о событии, имеющем отличную от нуля вероятность, но складывающемся из событий с нулевой вероятностью, не более парадоксально, чем представление об отрезке, имеющем определенную длину, тогда как ни одна точка отрезка отличной от нуля длиной не обладает. Отрезок состоит из таких точек, но его длина не равна сумме их длин.
Из этого свойства вытекает следующее следствие.
Следствие. Если Х – непрерывная случайная величина, то вероятность попадания этой величины в интервал (х1, х2) не зависит от того, является ли этот интервал открытым или закрытым:
P(x1 < X < x2) = P(x1 ≤ X < x2) = P(x1 < X ≤ x2) = P(x1 ≤ X ≤ x2).
Дата добавления: 2015-11-10; просмотров: 1650;
