Дисперсия случайной величины

Определение. Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

D(X) = M[X – M(X)]².

(5.9)

Для дискретной случайной величины X эта формула принимает вид:

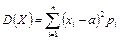(5.10)

Для непрерывной случайной величины:

(5.11)

На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D(X) = M(X²)– [M(X)]².

(5.12)

Для дискретной случайной величины X эта формула принимает вид:

(5.13)

Для непрерывной случайной величины:

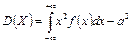(5.14)

Рассмотрим свойства дисперсии.

1. Дисперсия постоянной величины равна нулю:

D(С) = 0.

(5.15)

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.

D(kX) = k²D(X).

(5.16)

3. Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.

D(X + Y) = D(X) + D(Y).

(5.17)

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.

D(X – Y) = D(X) – D(Y).

(5.18)

Пример 5.2. Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.

Решение. Используя свойства дисперсии, находим

D(Z) = 8²D(X) – 5²D(Y) + D(7) = 64·1 + 25·2 + 0 = 114. ◄

Дата добавления: 2015-11-10; просмотров: 10225;