Б. Вычисление сил, действующих на плоскую наклонную стенку

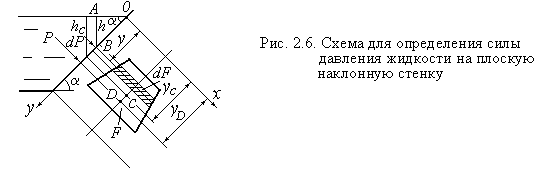
Рассмотрим сосуд с жидкостью, боковая стенка которого имеет угол

наклона α (рис. 2.6). На свободной поверхности p = p₀ . Пусть требуется определить силу давления на часть стенки произвольной формы. Введем систему координат и для выявления этой формы мысленно повернем стенку относительно оси оу).

На рассматриваемой части стенки с площадью F (будем называть ее плоской фигурой) выделим элемент поверхности dF. Он находится на глубине

h и отстоит от оси x на расстоянии y.

Будем учитывать только силу от действия жидкостного столба, так как здесь сила, создаваемая атмосферным давлением, действует на стенку с двух сторон. На площадку dF действует сила dP₂ = ρghdF, направленная нормально к стенке изнутри наружу.

Из чертежа видно, что 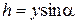, поэтому 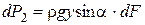. Найдем полную силу :

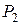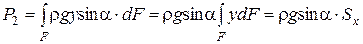. (2.24)

Здесь 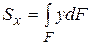− статический момент плоской фигуры относительно оси x .

Он вычисляется по формуле: 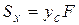, где y_c − координата центра тяжести плоской фигуры (на чертеже − точка с).

Окончательно получим: 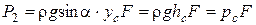. (2.25)

Здесь p_c − избыточное давление в центре тяжести плоской фигуры.

Полная сила Р₂ , действующая на фигуру, приложена к стенке в точке,

называемой центром давления (на чертеже − точка D). Координаты точек с

и D не совпадают.

Для определения координаты центра давления применим теорему Вариньона: для системы, находящейся в равновесии, момент результирующей силы относительно любой точки равен сумме моментов составляющих.

Момент dM одной из составляющих − силы dP₂ относительно точки О равен:

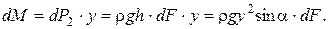(2.26)

Сумма моментов от составляющих − это интеграл вида

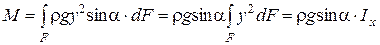, (2.27)

где 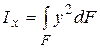− момент инерции фигуры относительно оси x.

С другой стороны, момент результирующей (силы Р₂) равен:

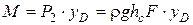. (2.28)

Приравняем (2.27 ) и (2.28):

.

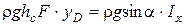Подставив 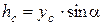и сократив на ρg, получим:

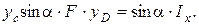Отсюда: 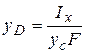. (2.29)

Обычно для различных фигур в справочниках даются центральные моменты инерции I_x0 относительно оси x₀, проходящей через центр тяжести. Связь между I_x и I_x0 выражается формулой: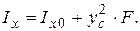

Отсюда 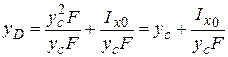. (2.30)

Из последней формулы следует, что центр давления всегда лежит ниже центра тяжести плоской фигуры. Если стенка горизонтальна, центр тяжести и

центр давления совпадают.

В ряде случаев полезным является построение эпюр распределения давления на плоские стенки. Примеры эпюр давления показаны на рис. 2.7.

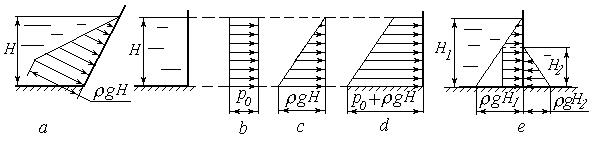
Рис. 2.7. Эпюры давления жидкости на плоские стенки:

а – эпюра давления от жидкостного столба на наклонную стенку; b, с, d – эпюры давления на вертикальную стенку соответственно атмосферного давления, давления жидкостного столба и суммарного давления; е – суммарная эпюра давления на вертикальную стенку при расположении жидкости по обе стороны стенки

Поскольку из основного закона гидростатики следует, что давление линейно зависит от глубины точки, эпюры получаются линейными; для их построения нужно знать давление в двух точках стенки. При построении эпюры величина давления в данной точке стенки в масштабе откладывается перпендикулярно к стенке в направлении от жидкости к стенке.