Силы, действующие в жидкости

Вследствие своей текучести (подвижности частиц) жидкость не может

сопротивляться действию сосредоточенных сил. В ней могут действовать только силы, распределенные либо по массе (массовые), либо по поверхности (поверхностные).

К массовым силам относятся силы собственного веса и силы инерции переносного движения. Единичной массовой силой 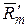называется массовая сила, действующая на единицу массы, или 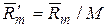. Физический смысл

единичной массовой силы − ускорение, вызванное этой силой. Проекции этого ускорения на координатные оси обозначаются X, Y, Z. Если речь идет об элементарной массе dM, то на нее действует такое же ускорение, как и на всю массу М. Следовательно, можно записать:

; ; .

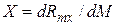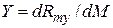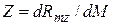Поверхностные силы действуют на границах выделенного объема жидкости со стороны жидкости, окружающей данный объем. Для выявления поверхностных сил применим метод сечений (рис. 2.1).

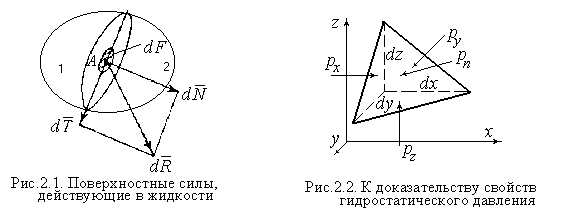
В выделенном объеме возьмем точку А и проведем через нее секущую плоскость, делящую объем на две части. Отбросим часть 1 и заменим ее силами, действующими со стороны объема 1 на объем 2. Эти силы распределены по секущей поверхности. В окрестности точки А рассмотрим

элементарную площадку dF. На нее действует сила 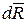. Разложим ее на две

составляющие − нормальную к площадке 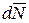и касательную 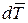. Обозначим

; .

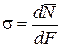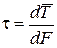Здесь σ − нормальное напряжение, τ− касательное напряжение.

Нормальное напряжение сжатия в жидкости называют давлением. В случае покоя жидкости касательные напряжения отсутствуют.

Давление в покоящейся жидкости называется гидростатическим.

Оно обладает двумя свойствами:

а) на границах выделенного объема жидкости силы, вызванные давлением, направлены по нормали внутрь рассматриваемого объема. Это объясняется тем, что жидкость практически неспособна сопротивляться растягивающим силам и может работать только на сжатие.

б) величина давления в данной точке объема не зависит от пространственной ориентации площадки dF.

Докажем последнее свойство. Выделим в жидкости элементарный объём в виде тетраэдра с рёбрами ∆x, ∆y, ∆z (рис. 2.2).

Пусть на жидкость внутри выделенного объёма действует единичная массовая сила, составляющие которой равны X,Y,Z. Под воздействием сил, действующих на грани тетраэдра, и массовой силы он находится в равновесии.

Масса тетраэдра равна произведению его объёма на плотность:

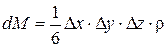(2.1)

Уравнение равновесия в проекции на ось x имеет вид:

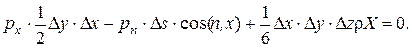(2.2)

Заметим, что 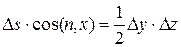;сократим уравнение (2.2) на .

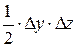Получим: 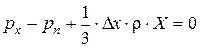. Аналогично для двух других осей:

;

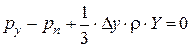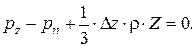
Положим 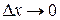, , 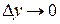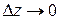. Тогда третий член, как бесконечно малый по сравнению с первым и со вторым, пропадёт, а p_x, p_y, p_z, p_n остаются.

В итоге из этих трех уравнений получаем: p_x= p_y= p_z= p_n .

Так как. направления осей были взяты произвольно, то по любым направлениям давление в точке будет одинаково. Поэтому гидростатическое давление можно рассматривать как скалярную величину. Таким же свойством обладает давление в движущейся идеальной жидкости.