Интегрирование дифференциального уравнения равновесия

А. Случай «абсолютного» покоя

Пусть в жидкости действуют из массовых сил только силы тяжести (рис. 2.4, а).

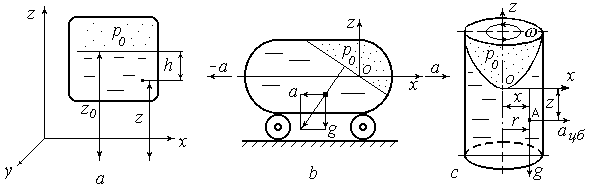
Рис. 2.4. К интегрированию уравнения равновесия:

a – «абсолютный» покой; b –движение сосуда с ускорением ; c – вращение сосуда

относительно вертикальной оси

В этом случае 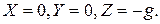Уравнение равновесия имеет вид:

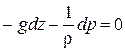. (2.9)

Интегрируем: 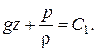Разделим левую и правую части на g:

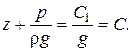(2.10)

Константу С найдем из граничного условия: на свободной поверхности (при z=z₀ ) p=p₀. Следовательно,

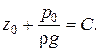(2.11)

Подставив полученное выражение для С в формулу ( 2.10 ), получим:

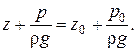(2.12)

Эту формулу называют основным законом гидростатики.

Найдем из этого выражения давление p в произвольной точке жидкости:

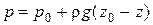. (2.13)

Из рис. 2.4, а следует, что z₀ − z = h, где h − глубина погружения рассматриваемой точки. Отсюда

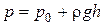. (2.14)

Это выражение также называют основным законом гидростатики, поскольку оно получено из выражения (2.12). Найдем уравнение свободной

поверхности для этого случая.

Подставив в формулу ( 2.8 ) 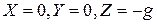, получим: .

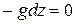После интегрирования получим: z = C (уравнение горизонтальной плоскости).

Б. Прямолинейное равноускоренное движение сосуда с жидкостью

Пусть сосуд с жидкостью движется равноускоренно вдоль горизонтальной оси х с постоянным переносным ускорением а (рис. 2.4, b). Прикладываем инерционное ускорение в обратном направлении в соответствии с принципом Д’Аламбера. После этого движущийся сосуд и жидкость в нем можно рассматривать находящимися в состоянии равновесия.

Выберем связанную с сосудом систему координат так, чтобы ее начало лежало на свободной поверхности жидкости. Тогда граничным условием будет:

при x =0, y = 0, z = 0 p = p₀ , где p₀ − давление среды над жидкостью.

Проекции единичной массовой силы будут равны: .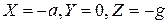

Подставив их в уравнение равновесия (2.6), получим

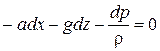. (2.15)

Сменив знак «−» на «+» и проинтегрировав, получим:

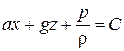. (2.16)

Константу С найдем из граничного условия: 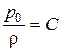. Подставим ее в (2.16 ):

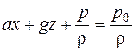. (2.17)

Найдем отсюда закон изменения давления в жидкости:

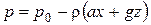. (2.18)

Для нахождения формы свободной поверхности можно использовать уравнение поверхности равного давления (2.8); можно также найти ее непосредственно из формулы (2.18), подставив в нее : .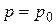

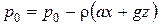Сократив на p₀ , получим:

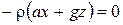. (2.19)

В этом выражении ρ ≠ 0, следовательно, ax+gz=0. Отсюда находим:

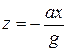. (2.20)

Это − уравнение наклонной плоскости (рис. 2.4, b).