Векторы электрического и магнитного полей. Материальные уравнения

Электрическое поле – особая форма материи, оказывающая силовое воздействие на электрические заряды. Магнитное поле – особая форма материи, оказывающая силовое воздействие на движущиеся электрические заряды. Электрическое и магнитное поля характеризуют с помощью силовых векторов.

Напряженность электрического поля Е определяют как силу, с которой электрическое поле действует на точечный положительный единичный заряд:

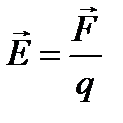(1.1)

Магнитная индукция определяется как сила, действующая со стороны магнитного поля на заряд единичной величины, движущийся с единичной скоростью:

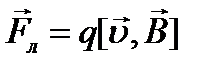(1.2)

Напряженность электрического поля в различных средах различна. Это объясняется следующим образом. Под действием электрического поля вещество создает собственное поле (поляризуется). Собственное поле вещества накладывается на внешнее, изменяя его.

Для характеристики поляризации вводят вектор поляризованности 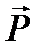. При не очень сильном внешнем поле величину вектора поляризованности можно считать пропорциональной напряженности электрического поля:

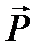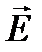= ε₀χ (1.3)

Входящий в формулу (1.3) безразмерный параметр χ характеризует среду и называется диэлектрической восприимчивостью среды.

При рассмотрении многих процессов удобно ввести вектор D, характеризующий независимое от свойств среды внешнее электрическое поле:

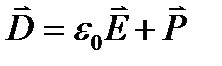. (1.3)

С учетом (1.2) формулу (1.3) можно представить в виде

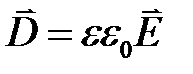, (1.4)

где ε = 1 + χ – относительная диэлектрическая проницаемость. Вектор 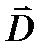принято называть вектором электрического смещения (электрической индукции). Иногда в литературе вводят абсолютную диэлектрическую проницаемость среды ε_А = .

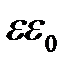Величина вектора 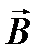зависит от свойств среды, поскольку под действием магнитного поля вещество намагничивается. В результате появляется дополнительное магнитное поле, которое налагается на первичное (явление, аналогичное поляризации вещества).

Намагниченность среды характеризуется вектором намагниченности 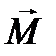. При рассмотрении многих процессов удобно вместо вектора 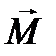ввести вектор 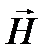, характеризующий независимое от свойств среды внешнее магнитное поле:

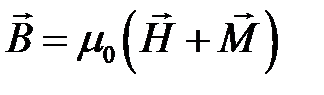(1.5)

где μ₀ = 4π ∙ 10^-7 Гн/м – постоянная величина, называемая магнитной постоянной. Вектор 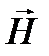принято называть вектором напряженности магнитного поля.

При не очень сильном внешнем магнитном поле можно считать, что вектор 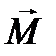пропорционален вектору .

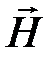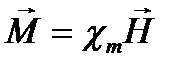(1.6)

Безразмерный коэффициент 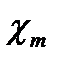называют магнитной восприимчивостью среды.

Подставляя формулу (1.6) в (1.5), получаем

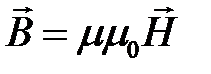(1.7)

где μ = 1 + χ_m – абсолютная магнитная проницаемость среды. Иногда в литературе вводят абсолютную магнитную проницаемость среды μ_А = .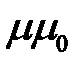

Под действием электрического поля в среде, обладающей проводимостью, возникает электрический ток (ток проводимости), распределение которого удобно характеризовать вектором плотности тока проводимости

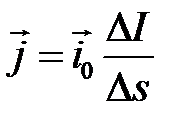(1.8)

где 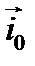– единичный вектор, показывающий направление тока (движения положительных зарядов) в рассматриваемой точке, Δs – плоская площадка, содержащая рассматриваемую точку, расположенная перпендикулярно вектору 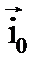, ΔI – сила тока проводимости, протекающего через Δs.

Вектор 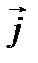связан с вектором 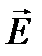соотношением

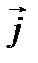= σ 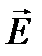, (1.9)

которое представляет собой закон Ома в дифференциальной форме. Коэффициент пропорциональности σ называют удельной проводимостью среды.

Система, состоящая из уравнений (1.4), (1.7), (1.9):

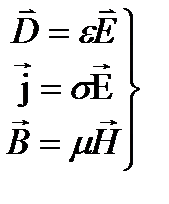(1.10)

имеет большое значение при изучении электромагнитных явлений, их часто называют материальными уравнениями, поскольку они характеризуют среду.