Уравнение непрерывности и закон сохранения зарядов

Из первого и третьего уравнений Максвелла вытекает важное соотношение, называемое уравнением непрерывности:

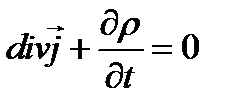(1.21)

Правая часть уравнения (1.28) представляет собой сумму плотностей тока проводимости и тока смещения, т.е. плотность полного тока 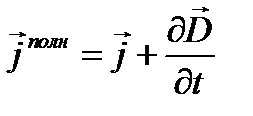, поэтому уравнение (1.28) эквивалентно условию div 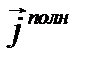= 0. Т. о. уравнение (1.28) показывает, что линии плотности полного тока являются непрерывными, в то время как линии плотностей токов проводимости и смещения могут иметь начало и конец.

Уравнение (1.21) можно переписать

I = -dQ/dt (1.22)

Уравнение (1.22) представляет собой закон сохранения заряда: всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток I, втекающий в эту область или вытекающий из нее.

Граничные условия

Рассматриваемая на практике область может состоять из двух (и более) разнородных сред. На границе раздела сред параметры e, m и s меняются скачком. Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными условиями. Данные соотношения получены по отдельности для нормальных (перпендикулярных) и тангенциальных (касательных) проекций электрических и магнитных векторов.

Граничное условие для нормальной составляющей вектора D в общем случае имеет вид:

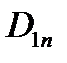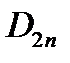- = τ. (1.23)

Здесь τ – поверхностная плотность заряда – характеризует заряд, распределенный вдоль поверхности раздела.

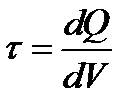(1.24)

В случае если заряд не сосредоточен на поверхности раздела, т.е. не является поверхностным, то правая часть формулы (1.24) равна нулю, а нормальная компонента вектора D непрерывна при переходе из одной среды в другую:

D_1n = D_2n (1.25)

Выражение (1.25) показывает, что при отсутствии на границе раздела двух сред поверхностных зарядов нормальная составляющая вектора электрического смещения меняется плавно, при наличии поверхностных зарядов – меняется скачкообразно.

Воспользовавшись материальным уравнением (1.4) можно получить граничное условие для напряженности электрического поля

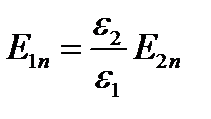(1.26)

Выражение (1.26) показывает, что нормальная составляющая вектора напряженности электрического поля меняется скачком.

Граничное условие для нормальной составляющей вектора магнитной индукции имеет вид

B_1n = B_2n (1.27)

Выражая в равенстве (1.27) B_n через Н_n, получаем

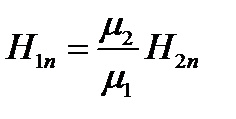(1.28)

Граничное условие для касательных составляющих вектор напряженности магнитного поля имеет вид:

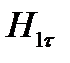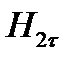- =j_sl. (1.29)

j_sl – плотность поверхностного тока. Она определяется соотношением:

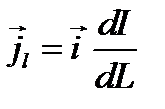(1.30)

Выражение (1.30) характеризует токи, распределенные вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие токи называют поверхностными.

В случае отсутствия поверхностных токов можем записать:

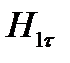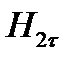= . (1.31)

Выражение (1.31) показывает, что при отсутствии на границе раздела двух сред поверхностных токов касательная составляющая вектора напряженности магнитного поля меняется плавно, при наличии поверхностных токов – меняется скачкообразно.

Касательная составляющая вектора В, наоборот, претерпевает разрыв, величина которого определяется отношением магнитных проницаемостей:

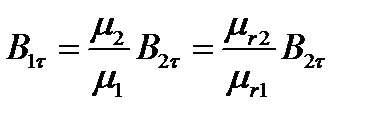(1.32)

Граничное условие для касательной составляющей вектора Е:

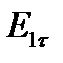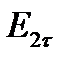= . (1.33)

Касательная составляющая вектора Dпретерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями:

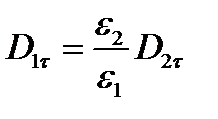(1.34)