Основные уравнения электромагнитного поля – уравнения Максвелла
Первое уравнение
Все электромагнитные процессы, относящиеся к макроскопической электродинамике, подчиняются законам (уравнениям), впервые сформулированным Максвеллом. Эти уравнения были получены в результате обобщения накопленных к тому времени экспериментальных данных и называются уравнениями Максвелла.
Первое уравнение Максвелла является обобщением закона полного тока: циркуляция вектора напряженности Н магнитного поля по замкнутому контуру L равна сумме тока I, пронизывающего данный контур, и потока величины 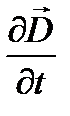 через площадку, ограниченную контуром:
через площадку, ограниченную контуром:
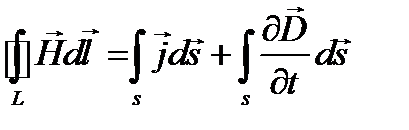 (1.11)
(1.11)
| Рис.1.1 |
 где
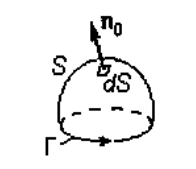
где 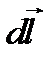 – элемент контура L, направленный по касательной к L, положительное направление которого выбирается в соответствии с обходом контура L; S - произвольная поверхность, опирающаяся на контур L, направление вектора
– элемент контура L, направленный по касательной к L, положительное направление которого выбирается в соответствии с обходом контура L; S - произвольная поверхность, опирающаяся на контур L, направление вектора 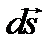 связано с направлением обхода контура L правилом правой руки (рис. 1.1).
связано с направлением обхода контура L правилом правой руки (рис. 1.1).
Величина 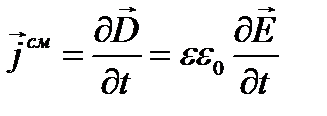 представляет собой скорость изменения электрического поля в контуре и носит название тока смещения. Введение этой величины обусловлено возникновением магнитного поля в присутствии переменного электрического. Кроме того, в случае замыкания конденсатора в цепь переменного электрического тока (в отличие от постоянного) приводит к тому, что цепь является замкнутой. Токи проводимости протекают в проводящих средах, токи смещения – в диэлектриках. Сумма тока смещения и тока проводимости носит название полного тока.
представляет собой скорость изменения электрического поля в контуре и носит название тока смещения. Введение этой величины обусловлено возникновением магнитного поля в присутствии переменного электрического. Кроме того, в случае замыкания конденсатора в цепь переменного электрического тока (в отличие от постоянного) приводит к тому, что цепь является замкнутой. Токи проводимости протекают в проводящих средах, токи смещения – в диэлектриках. Сумма тока смещения и тока проводимости носит название полного тока.
Уравнение (1.11) представляет собой первое уравнение Максвелла в интегральной форме. Этот закон можно сформулировать также в дифференциальной форме:
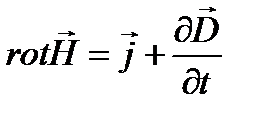 (1.12)
(1.12)
Запись 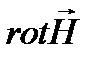 – ротор вектора
– ротор вектора 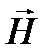 – математический оператор, характеризующий завихренность вектора.
– математический оператор, характеризующий завихренность вектора.
Дата добавления: 2015-11-10; просмотров: 929;
