Дифференциальные уравнения движения идеальной жидкости

Выделим в движущейся идеальной (невязкой) жидкости элементарный

объем в виде параллелепипеда со сторонами dx, dy, dz (рис. 4.1).

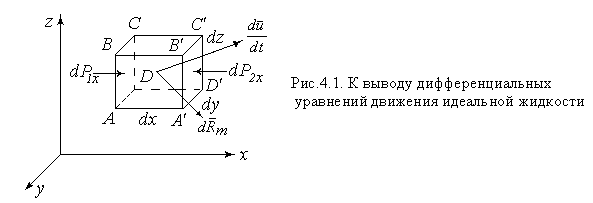
На выделенный элемент действует массовая сила 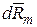и поверхностные

силы давления, направленные нормально к граням внутрь объема.

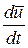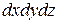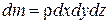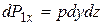Касательные поверхностные силы (силы трения) отсутствуют, так как жидкость невязкая. Элемент движется с ускорением . Его объем равен , а масса . Составим уравнение движения в проекции на ось х. Будем считать, что по бесконечно малой площадке давление распределено равномерно и равно среднему давлению (давлению в центре грани). На грань действует давление p и вызванная им сила . На грань действует давление . 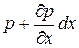Оно создает силу 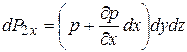, направленную противоположно оси x.

Единичная массовая сила, действующая в жидкости, имеет составляющие X,Y,Z. Проекция массовой силы 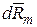на ось х будет равна .

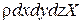Итак, уравнение движения в проекции на ось х запишется в виде:

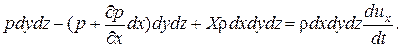(4.1)

Открыв скобки, сократив на не равное нулю произведение 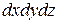и разделив на ρ, получим: 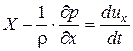. Аналогично выглядят проекции уравнения равновесия на другие оси. В итоге получим систему дифференциальных уравнений движения (уравнений Эйлера), имеющую вид:

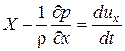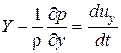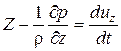; ; . (4.2)

Для решения этой системы сведём её к одному уравнению. Для этого умножим первое на dx, второе на dy, третье на dz и сложим все три уравнения: 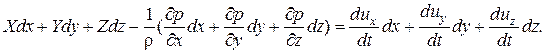. (4.3)

Рассмотрим установившееся движение. Тогда выражение в скобках является полным дифференциалом функции 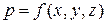, то есть dp .

Рассмотрим отдельно правую часть уравнения (4.3).

.

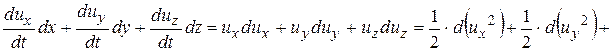
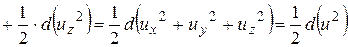Таким образом, из (4.3) получим:

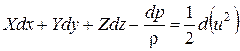. (4.4)

Полученное выражение является дифференциальным уравнением

движения идеальной жидкости.

Пусть из массовых сил на элемент объема действует только сила тяжести. Тогда 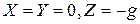. Подставим это в (4.4).

.

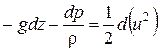Перенесем правую часть влево и сменим знаки «минус» на «плюс»:

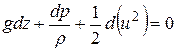. (4.5)

Интегрируя (4.5), получим:

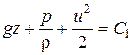или 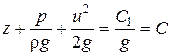. (4.6)

Полученное общее решение называется интегралом Бернулли.

Так как бесконечно малый объем движется вдоль линии тока,

то во всех живых сечениях элементарной струйки сумма трех слагаемых левой части выражения (4.6) является постоянной величиной. Для любых двух сечений с индексами 1 и 2 можно записать:

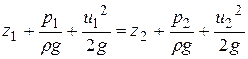. (4.7)

Это уравнение называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Элементарная струйка с параметрами в сечениях 1 и 2 показана на рис. 4.2, а.

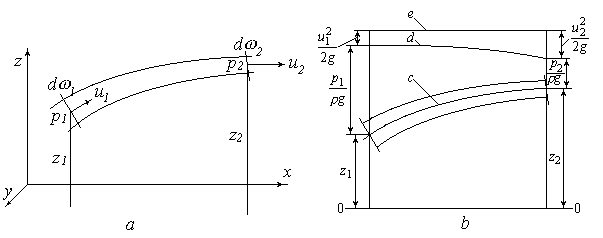
Рис.4.2. К уравнению Бернулли:

а – схема элементарной струйки ; b – к геометрическому толкованию

Энергетическое толкование уравнения Бернулли. Удельной энергией Е_уд

(напором) называется энергия жидкости, отнесенная к единице веса, или

Е_уд = Е / G .Поскольку Е измеряется в Дж (Н∙м), то размерность Е_уд равна м.

Так как все слагаемые уравнения Бернулли имеют размерность м, каждое из них представляет собой некоторую удельную энергию: z – удельную потенциальную энергию положения, p/ρg – удельную потенциальную энергию давления, u² /2g – удельную кинетическую энергию. Поэтому уравнение Бернулли − это закон сохранения удельной энергии и формулируется так:

В любом сечении элементарной струйки идеальной жидкости сумма

удельной потенциальной и кинетической энергии – величина постоянная.

Геометрическое толкование уравнения Бернулли. Поскольку все слагаемые уравнения Бернулли имеют размерность м, их величину можно откладывать на графике в определенном масштабе. Величина z называется геодезической высотой, p/ρg − пьезометрической высотой, сумма z + p/ρg – потенциальным напором Н_р , u² /2g – скоростной высотой (скоростным напором), сумма

z + p/ρg+ u² /2g – полным напором Н.

На рис. 4.2, b показаны графики изменения этих величин вдоль элементарной струйки идеальной жидкости: с – геодезической высоты, d –

потенциального напора, е – полного напора. Вместо плоскости x0y рисуют ее след – горизонтальную линию 0 − 0. Она называется плоскостью сравнения.

Линия полного напора при движении вдоль элементарной струйки идеальной жидкости – горизонтальная прямая. В этом и заключается геометрическое толкование уравнения Бернулли.

В реальной (вязкой) жидкости вследствие трения между соседними струйками, имеющими различные скорости, происходит выделение тепла и

его передача в окружающую среду (диссипация энергии). Поэтому напор в

сечении струйки, расположенном ниже по течению, будет меньше, чем в вышележащем. Уравнение Бернулли записывается в следующем виде:

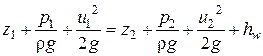. (4.8)

Здесь h_w – гидравлические потери.