Уравнение Бернулли для потока жидкости

Рассмотрим установившееся движение плавно изменяющегося потока вязкой несжимаемой жидкости (рис. 4.3). Считаем, что температура потока не изменяется вследствие тепловых процессов (поток изотермический).

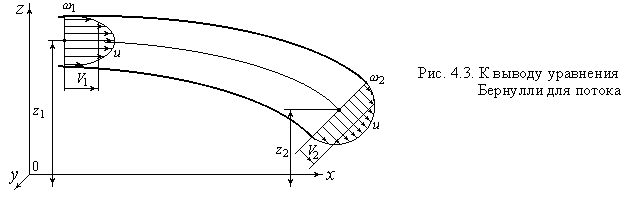
Прежде всего рассмотрим, как изменяется давление по сечению потока.

Для простоты возьмем сечение ω₁, расположенное горизонтально.

Так как скорости u в этом сечении параллельны оси х, то

.

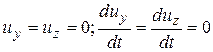Тогда система дифференциальных уравнений примет вид:

; ; .

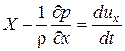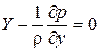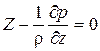Последние два уравнения описывают изменение давления в плоскости x0y

и полностью совпадают с соответствующими уравнениями равновесия (2.4).

Следовательно, в плоскости x0y (в плоскости живого сечения потока) давление распределяется по закону гидростатики (2.10):

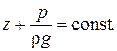(4.9)

Энергия dE жидкости, протекающей через живое сечение элементарной струйки за единицу времени, равна:

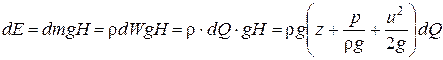. (4.10)

Чтобы получить полную энергию всего потока, нужно просуммировать

(проинтегрировать) энергию всех струек, проходящих через сечение ω:

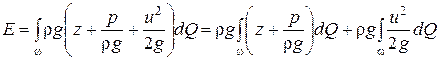. (4.11)

Для двух сечений потока уравнение сохранения полной энергии

(в случае, если бы жидкость была идеальной) имеет вид:

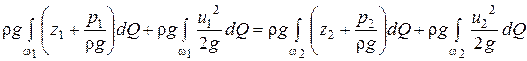. (4.12)

Гидравлические потери удельной энергии струйки равны h_w . Потери полной энергии учтем, считая, что h_w − средние потери напора в сечении (одинаковые для всех струек). Тогда гидравлические потери полной энергии потока равны 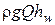. С учетом этого выражение (4.12) примет вид:

.

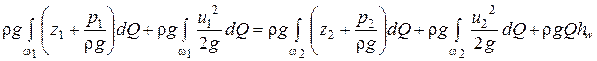Это выражение называется уравнением энергии потока вязкой жидкости в интегральной форме.

Так как для сечений 1 и 2 справедливо выражение (4.9), то первый интеграл в левой и правой части можно переписать в виде

.

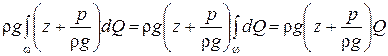Второй интеграл можно преобразовать следующим образом:

.

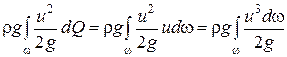Тогда уравнение энергии в интегральной форме примет вид

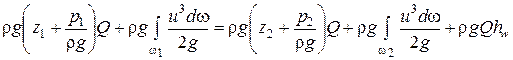. (4.13)

Перейдем снова к удельной энергии, разделив уравнение (4.13) на ρgQ.

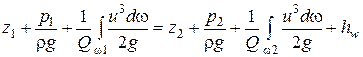(4.14)

Учтя, что 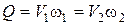, и умножив/разделив третье слагаемое в левой и правой частях этого выражения соответственно на 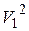и 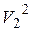, получим

.

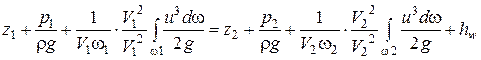Введем обозначения:

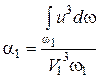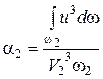; . (4.15)

Коэффициенты α₁ и α ₂ учитывают влияние формы эпюры скоростей

на удельную кинетическую энергию потока и называются коэффициентами

Кориолиса. С учетом этого выражение (4.15) примет вид:

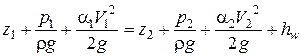. (4.16)

Это выражение носит название уравнения Бернулли для потока вязкой жидкости и широко применяется в расчетах установившегося движения.