Гидравлические устройства, основанные на применении

Уравнения Бернулли

Расходомер Вентурислужит для измерения расхода жидкости в трубопроводах и представляет собой плавное сужающее устройство, монтируемое как врезка в трубопровод (рис. 4.7, а). К широкому сечению трубки Вентури площадью ω₁ и узкому площадью ω₂ присоединены трубки дифференциального манометра ДМ, измеряющего разность давлений Δр в этих сечениях.

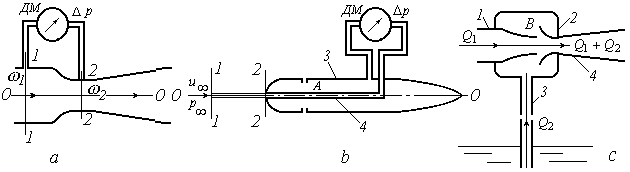
Рис. 4.7. Гидравлические устройства, основанные на применении уравнения Бернулли:

а – расходомер Вентури; b – трубка Пито−Прандтля; с− эжекционный насос

Запишем уравнение Бернулли для сечений 1−1 и 2−2 (плоскость сравнения 0 − 0, z₁ = z₂ = 0, гидравлическими потерями пренебрегаем):

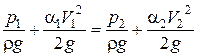. (4.21)

Так как по уравнению постоянства расхода 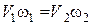, то .

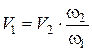Подставив это в (4.21) и сократив на g, получим:

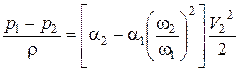. (4.22)

Обозначив 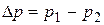, из (4.22) найдем V₂ :

.

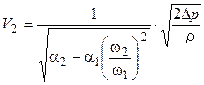Найдем расход:

.

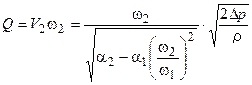Введем сюда коэффициент μ , учитывающий уменьшение расхода из-за

гидравлических потерь, и окончательно получим: 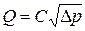, где

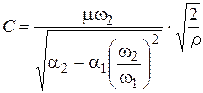− постоянная прибора.

Таким образом, расходомер Вентури измеряет расход через определение перепада давлений Δр.

Трубка Пито − Прандтля(рис. 4.7, b) предназначена для измерения местной жидкости или газа в каналах, а также для измерения скорости движения тела относительно неподвижной жидкости (газа) – например, скорости судна или самолета.

Она состоит из пустотелого обтекаемого корпуса 3 с отверстиями на боковой поверхности. В корпусе помещается приемник полного давления − трубка 4, направленная своим отверстием навстречу набегающему потоку.

Обозначим параметры невозмущенного потока (параметры на таком расстоянии от носика трубки , при котором не наблюдается влияние самой трубки на поток) через 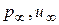. Рассмотрим элементарную струйку, текущую

по оси трубки. Сечение 1−1 соответствует параметрам невозмущенного потока, сечение 2−2 – месту встречи струйки с входом в приемник полного давления.

Составим уравнение Бернулли для сечений струйки 1−1 и 2−2, считая ее идеальной (пренебрегая гидравлическими потерями). Скорость в сечении 2−2 равна нулю, так как струйка тормозится, ударяясь в неподвижную жидкость, заполняющую трубку 4; z₁ = z₂ = 0.

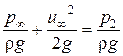. (4.23)

Опыты показывают, что в полости А трубки устанавливается давление,

весьма близкое к давлению невозмущенного потока 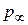. Поэтому она называется приемником статического давления.

Из формулы (4.23) легко получить:

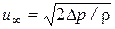, где 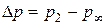. (4.24)

Величина перепада давлений Δр измеряется дифференциальным манометром.

Эжекционный насос (элеватор)состоит из трубки 1, имеющей на конце плавное сужение, камеры смешения 2 и постепенно расширяющейся трубки 4,

входное отверстие которой расположено на небольшом расстояния от выхода из трубки 1 в камере 2 (рис. 4.7, с). По трубке 1 в камеру смешения подается расход несущей жидкости Q₁. Из-за сужения трубки 1 скорость в ее выходном сечении растет, а давление (в соответствии с уравнением Бернулли) падает. Одновременно давление падает во всей полости В. Благодаря этому жидкость из водоема, резервуара или другой трубы, где давление меньше давления в

камере 2, засасывается в нее по трубке 3 с расходом Q₂. В полости В происходит слияние и перемешивание потоков; суммарный поток с расходом

Q₁ + Q₂ выходит по трубке 4 и движется далее по трубопроводу.

Кавитация

Кавитация – явление , возникающее в жидкости при больших скоростях движения, а следовательно, при малых давлениях.

Рассмотрим движение жидкости по трубопроводу (рис. 4.8).

Запишем уравнение Бернулли для сечений 1−1 и 2−2 потока реальной жидкости. Скоростью в баке пренебрегаем (V₁ =0), z₁ = h, p₁ =p₀ , z₂ =0.

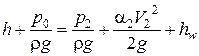. (4.25)

Отсюда найдем V₂ :

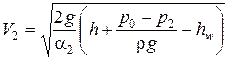. (4.26)

Из формулы (4.26) видно, что скорость V₂ увеличивается с уменьшением

давления. Она будет максимальной при минимально возможном давлении.

Для жидкости это давление насыщенного пара р_нп . Потому 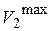можно

найти из (4.26), подставив в нее :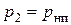

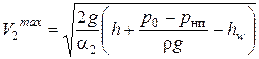. (4.27)

При достижении средней скорости потока 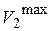(например, за счет выбора слишком малого диаметра трубопровода или установки в трубопроводе сужающего устройства с очень малым проходным сечением) и понижении давления до 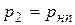в жидкости наступает кипение − выделение пузырьков пара по всему объему. Поток превращается в двухфазный (пар + жидкость),

сплошность его нарушается. Этот процесс и называется кавитацией.

Кавитация полностью нарушает процесс транспортировки жидкости.

Она развивается постепенно, в несколько стадий (рис. 4.9, a , b, c). Вначале выделяются пузырьки пара (а); они всплывают и объединяются в более крупные пузыри (b); далее происходит образование обширных объемов пара −

паровых каверн (с).

Помимо нарушения процесса транспортировки кавитация вредна еще тем, что вызывает повышенный износ материалов − «кавитационную коррозию».

Предположим, что кавитационный поток с паровой каверной попадает в расширяющуюся часть трубопровода − сечение 1−1 (рис. 4.9, d).

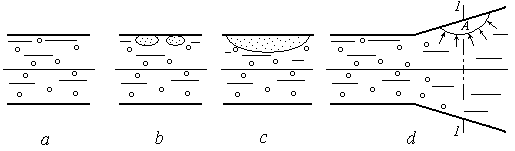
Рис.4.9. Стадии кавитации

Поскольку скорость уменьшается, давление становится больше р_нп ;

кипение быстро прекращается. Пар в каверне мгновенно конденсируется;

образующаяся жидкость оседает на стенке и впитывается окружающей жидкостью. Поскольку объем конденсата во много раз меньше объема каверны, в ней возникает пустое пространство, в которое с большой скоростью устремляется окружающая жидкость. При соударении движущейся жидкостью со стенкой возникает резкое местное повышение давления (гидравлический удар). Этот процесс называется «схлопыванием» каверны. Такой же процесс схлопывания происходит в отдельных пузырьках пара, касающихся стенки.

Многократно повторяющиеся гидравлические удары вызывают откол мельчайших частиц металла и в итоге − кавитационную коррозию.

Особенно опасна кавитационная коррозия в элементах гидроарматуры (где поток жидкости проходит через узкие щели и малые проходные сечения),

гидромашинах с быстровращающимися роторами (центробежных насосах, гидротурбинах), в судовых винтах.

Меры борьбы с кавитацией: недопущение высоких скоростей жидкости в трубопроводах; повышение рабочего давления в гидросистемах (например, применение наддува баков сжатым воздухом); недопущение превышения

точки расположения всасывающего отверстия центробежного насоса выше

допустимого значения; применение кавитационностойких материалов.