Гидравлический удар

Гидравлическим ударом называется особый вид неустановившегося движения жидкости в трубопроводе − колебательный процесс изменения

давления, возникающий при быстром закрытии или открытии задвижки, при внезапной остановке насоса или его включении при открытом затворе на нагнетательной линии, а также в некоторых других случаях.

Резкое повышение давления при гидравлическом ударе может вызвать

разрушение трубопровода, понижение до р_нп – кавитацию.

Теоретическое и экспериментальное исследование гидравлического удара

было выполнено Н.Е. Жуковским в 1898 г. Он получил формулу для ударного повышения давления и его связь с упругими характеристиками как жидкости, так и материала трубопровода.

Стадии развития гидравлического удара в трубопроводе при резком закрытии задвижки показаны на рис. 4.10 (гидравлическими потерями пренебрегаем).

1. Задвижка открыта, давление на входе в трубу и по всей его длине равно ,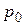

средняя скорость равна .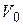

2. Задвижка резко закрылась. У задвижки жидкость затормозилась ( ),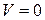

давление резко поднялось ( 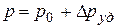). Упругий трубопровод в этом месте расширился. Зона заторможенной жидкости перемещается справа налево со скоростью с (скорость ударной волны).

3.Ударная волна дошла до бака. Во всем трубопроводе , .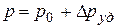

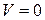Весь трубопровод расширился.

4. Так как в трубопроводе давление больше, чем в баке, жидкость начинает вытекать из трубы в бак. Так как пренебрегаем гидравлическими потерями, потенциальная энергия давления, переходя обратно в кинетическую, создает

скорость течения, равную 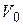, но направленную в обратную сторону. В области трубы, из которой жидкость вытекает, давление падает обратно до 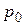, труба принимает первоначальный диаметр. Эта область перемещается слева направо со скоростью с.

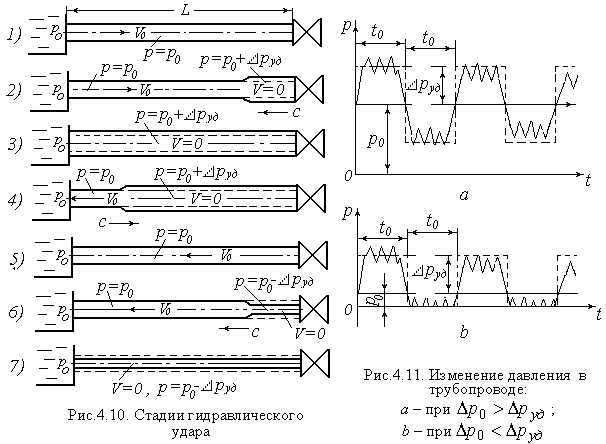
5. Ударная волна дошла до задвижки. Весь трубопровод имеет начальный диаметр, давление в нем равно 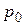, скорость равна − .

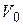6. Так как жидкость оттекает от задвижки, перед ней создается разрежение (давление падает до 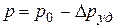). Жидкость в этой зоне останавливается

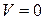( ), диаметр трубы становится меньше начального. Эта зона перемещается справа налево со скоростью с.

7. Ударная волна дошла до бака. Во всем трубопроводе , .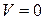

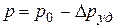Так как давление в трубе меньше, чем в баке, начинается движение жидкости из бака в трубу, и весь цикл повторяется.

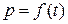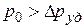Если перед задвижкой установить датчик, непрерывно регистрирующий давление, то график при выглядит так, как на рис. 4.11, а.

Пунктиром показан теоретический график, сплошной линией − реальный.

В опытах Н.Е. Жуковского было зафиксировано до 12 полных циклов. С течением времени колебания затухают.

Время прохождения ударной волной расстояния от задвижки до бака и обратно называется фазой гидравлического удара 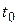. Она равна .

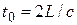Если 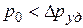, то при отрицательной амплитуде давление в трубопроводе может понизиться только до 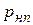, что чревато возникновением кавитации.

При теоретическом анализе гидравлического удара Н.Е. Жуковский использовал теорему о количестве движения из теоретической механики:

изменение количества движения тела массой m за промежуток времени 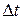равно импульсу равнодействующей приложенных к телу внешних сил.

Эта теорема широко применяется в гидродинамике, позволяя решать разнообразные задачи.

Напомним, что количеством движения называется произведение ,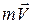

а импульсом силы 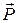− произведение .

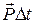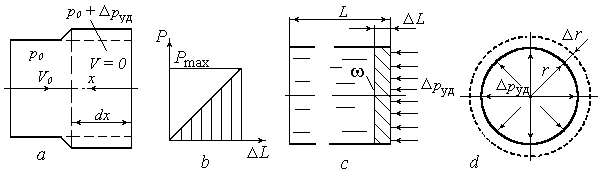
Рис. 4.12. К выводу формулы Н.Е. Жуковского

Рассмотрим стадию 2 (рис. 4.10). Область трубопровода, примыкающая к границе зоны, где жидкость остановилась, и зоны, где она продолжает двигаться, показана на рис. 4.12, а. Изменением площади сечения трубопровода 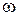будем пренебрегать, так как оно мало. За время 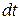ударная волна прошла в в направлении оси х путь 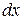. У массы 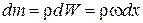в момент времени t скорость была равна: 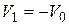(так как скорость направлена противоположно оси х). В момент времени 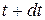скорость равна: 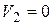(жидкость в этом объеме остановилась). Значит, изменение количества движения массы 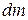равно:

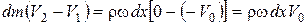. (4.28)

Справа на объем массой 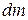действует давление 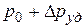, слева − .

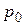Следовательно, результирующая сила Р равна :

.

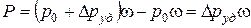Импульс этой силы равен :

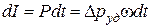. (4.29)

Приравняем (4.28) и (4.29). .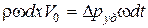

Сократим левую и правую части на ω и разделим на dt : .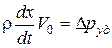

Учтя, что 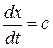(скорость ударной волны), получим формулу Н.Е. Жуковского:

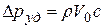. (4.30)

Определим скорость ударной волны для упругого трубопровода. До закрытия задвижки кинетическая энергия всей жидкости в трубе равна:

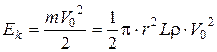. (4.31)

Рассмотрим работу деформации жидкости и трубы. При нагружении упругого тела силой Р зависимость величины этой силы от деформации ΔL

в пределах закона Гука линейна (рис. 4.12, b), а работа деформации равна площади заштрихованного треугольника под прямой:

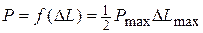. (4.32)

При подъеме давления до 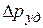появилась сила 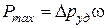, сжимающая жидкость в трубопроводе на величину ΔL (рис. 4.9, с).

Работа деформации жидкости на основе формулы (4.32) равна:

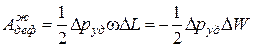, (4.33)

где 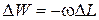, так как изменение объема имеет отрицательный знак.

Из формулы (1.4) имеем ( ):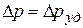

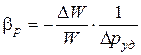, или .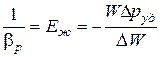

Отсюда получим:

.

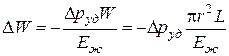Подставим это выражение в формулу (4.33):

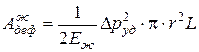. (4.34)

Работа деформации трубы (увеличения ее радиуса из-за увеличения давления) вычисляется также на основе формулы (4.32). При этом считаем,

что полная сила, стремящаяся расширить трубу и действующая по радиусу (она распределена по всей боковой поверхности трубы), равна (рис. 4.12, d): 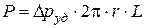. Удлинение вдоль линии действия силы − это 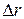. Поэтому

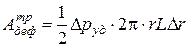. (4.35) Запишем закон Гука: 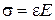. (4.36)

Здесь 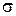− нормальное напряжение, 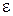− относительное удлинение, в нашем случае равное 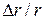, Е − модуль упругости материала.

Из сопротивления материалов известна формула для вычисления напряжения 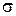в цилиндрической оболочке, нагруженной внутренним давлением (в нашем случае :

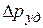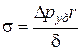, где δ− толщина стенки. (4.37)

Приравняем (4.36) и (4.37):

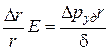, или .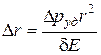

Подставим это выражение в (4.35) и получим:

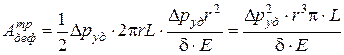. (4.38)

При гидравлическом ударе кинетическая энергия жидкости в трубе расходуется на работу деформации жидкости и трубы. Поэтому

.

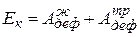С учетом (4.31), (4.34) и (4.38) получим:

.

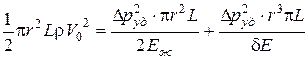Сократив на 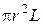и взяв за скобки 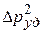, получим:

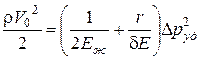, или .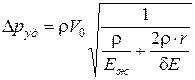

Сопоставив последнее выражение с формулой (4.30), найдем:

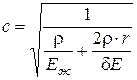(4.39)

Величина скорости ударной волны близка к скорости звука с₀ в жидкости

и для воды составляет 900 – 1400 м/с (с₀ = 1425 м/с).

Если время закрытия (открытия) задвижки 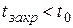, гидравлический удар называется прямым и для расчета Δр_уд применяется формула Жуковского. Если 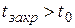, гидравлический удар называется непрямым. Ударное повышение давления 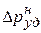для него меньше и может быть определено по формуле:

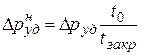_. (4.40)

Здесь 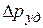− ударное повышение при прямом ударе.

Меры борьбы с гидравлическим ударом: увеличение времени закрытия и открытия задвижек, установка на трубопроводе уравнительных резервуаров и воздушных колпаков, предохранительных клапанов, обратных клапанов после насоса и непосредственно на трубопроводе для подачи в него атмосферного воздуха или жидкости из вспомогательного трубопровода (при падении давления ниже р₀), а также установка специальных клапанов – демпферов.

Гидравлический удар имеет также полезное применение – на его принципе построен специальный вид насосов – гидравлический таран.