Анализ одномерных потоков несжимаемой жидкости и газа.
Функция Лейбензона для несжимаемой жидкости
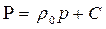 (40)
(40)
Для совершенного газа
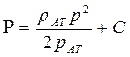 (41)
(41)
Прямолинейно – параллельный поток несжимаемой жидкости и совершенного газа
Подставим в (32), (34), (36*) выражение функции Лейбензона (40), тогда
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Функция Лейбензона | 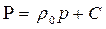
| 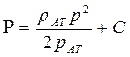
|
| Распределение давления по пласту 0 £ x £ L | 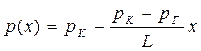 (42) (42)
| 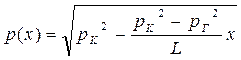 (43)
(43)
|
| Массовый расход Qm | 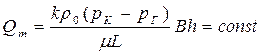 (44)
(44)
| 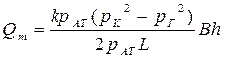 (45)
(45)
|
| Массовая скорость фильтрации | 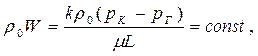 (46)
(46)
| 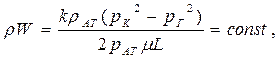 (47)
(47)
|
| Объемный расход Q | 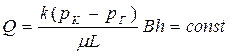 (48) (48)
| 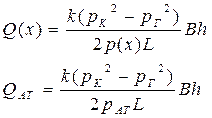 (49)
(49)
|
| Скорость Фильтрации (объемная) | 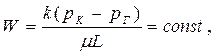 (50)
(50)
| 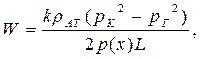 (51)
(51)
|
| Средневзвешенное давление | 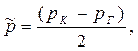 (52)
(52)
| 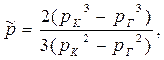 (53)
(53)
|
| Время движения Отмеченных Частиц t | 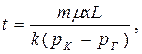 (54)
(54)
| 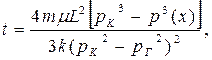 (55)
(55)
|
| Время продви – жения до Галереи Т | 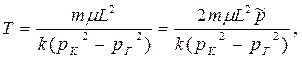 (56)
(56)
| 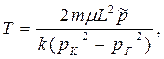 (57)
(57)
|
Плоскорадиальный фильтрационный поток
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Распределение давления по пласту | 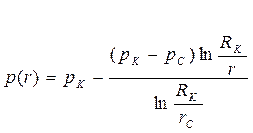 (58)
(58)
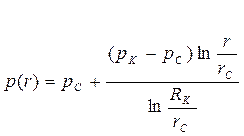 (60)
(60)
| 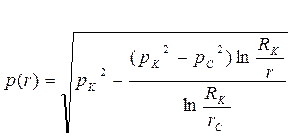 (59)
(59)
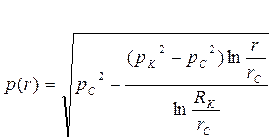 (61)
(61)
|
| Массовый расход Qm | 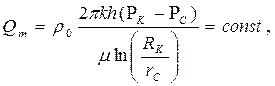 (62) (62)
| 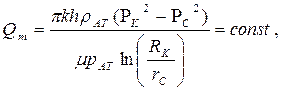 (63)
(63)
|
| Массовая скорость фильтрации rW | 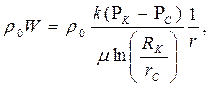 (64)
(64)
| 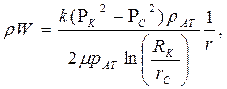 (65)
(65)
|
| Объемный расход Q | 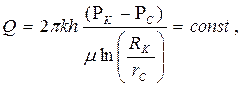 (66)
(66)
| 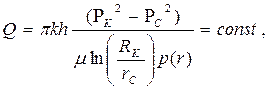 (67)
(67) 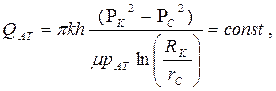 (68)
(68)
|
| Объемная скорость фильтрации | 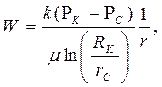 (69)
(69)
| 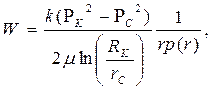 (70)
(70)
|
| Средневзвешенное давление | 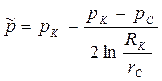 (71)
(71)
| 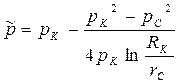 (72)
(72)
|
| Время движения отмеченных частиц | 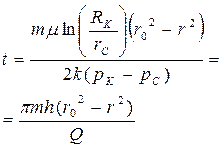 (73)
(73)
|
 ________________ ________________
|
| Время движения частицы от контура до забоя Т | 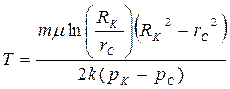 (74)
(74)
| 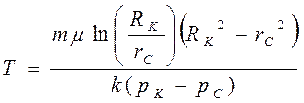 (75) (75)
|
Для несжимаемой жидкости давление меняется вдоль координаты r по логарифмическому закону (Рис.5, кривая 1). Вращение кривой p(r) в пространстве вокруг оси скважины образует поверхность, называемую воронкой депрессии.
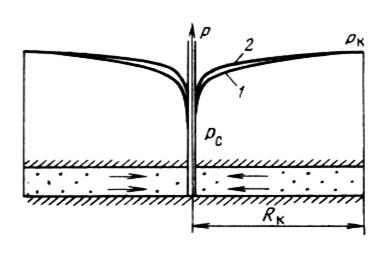 |
Рис. 5. Кривые распределения давления в плоскорадиальном потоке:
1 – для жидкости, 2 – для газа.
Зависимость дебита от перепада давления 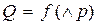 называется индикаторной линией. В потоке жидкости по закону Дарси индикаторная линя – прямая (Рис. 6).
называется индикаторной линией. В потоке жидкости по закону Дарси индикаторная линя – прямая (Рис. 6).
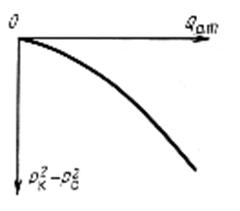 Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Qm к перепаду давления Dр называется коэффициентом продуктивности скважины k. Рис. 6.
Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Qm к перепаду давления Dр называется коэффициентом продуктивности скважины k. Рис. 6.
Из (60) следует, (для жидкости):
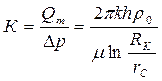 ,
,
коэффициент продуктивности определяется в результате исследования скважины при установившихся отборах.
Радиально – сферический фильтрационный поток несжимаемой жидкости и совершенного газа.
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Распределение давления р(r) | 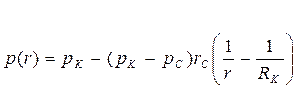 (76) (76)
| 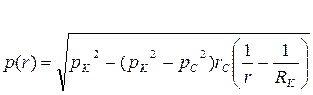 (77) (77)
|
| Массовый расход Qm | 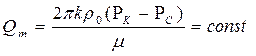 (78)
(78)
| 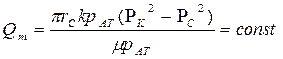 (79)
(79)
|
| Массовая ско –рость фильтрации | 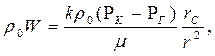 (80)
(80)
| 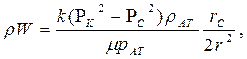 (81)
(81)
|
| Объемный расход | 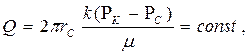 (82)
(82)
| 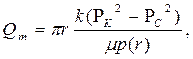 (83)
(83)
|
| Объемная скорость фильтрации | 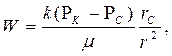 (84)
(84)
| 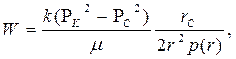 (85)
(85)
|
| Время движения частиц t | 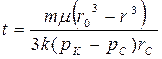 (86)
(86)
| ______________ |
| Время движения от контура до забоя | 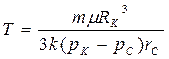 (87) (87)
| 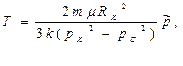 (88)
где (88)
где 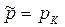
|
Фильтрация по степенному закону
При плоскорадиальном движении закон приобретает вид:
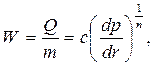
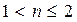 ,
, 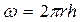 ,
,
где с и n – константы, определяемые из опыта или по результатам исследования скважины.
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Распределение давления р(r) | 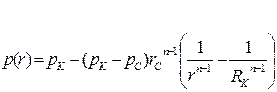 (90)
(90)
| 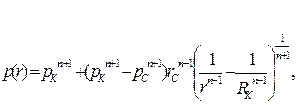 (91)
(91)
|
| Массовый Расход | 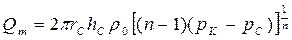 (92)
(92)
| 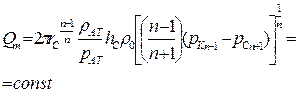 (93)
(93)
|
| Распределение давления р(r) | 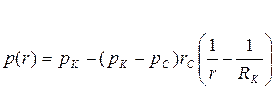 (94)
(94)
| 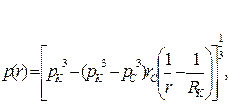 (95)
(95)
|
| Массовый расход Qm | 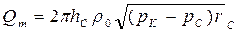 (96)
(96)
| 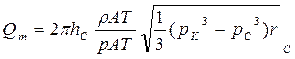 (97)
(97)
|
Массовый расход для жидкости пропорционален депрессии в степени 1/n, поэтому индикаторная линия 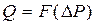 при 1< n < 2 будет иметь вид выпуклой к оси дебитовстепенной кривой с дробным показателем меньшим 2. В случае фильтрации по закону Краснопольского, индикаторная линия является параболой второго порядка.
при 1< n < 2 будет иметь вид выпуклой к оси дебитовстепенной кривой с дробным показателем меньшим 2. В случае фильтрации по закону Краснопольского, индикаторная линия является параболой второго порядка.
Рис. 7. Индикаторнаые линии,
соответствующие различным
законам фильтрации жидкости.
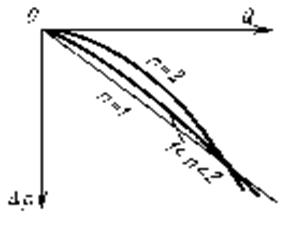
Рис. 7.
Фильтрация по двучленному закону.
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Функция Лейбензона | 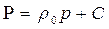
| 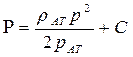
|
| Распределение Давления | 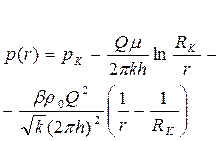 (98)
(98)
| 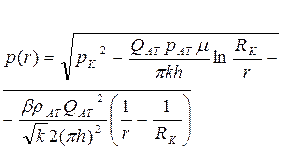 (99)
(99)
|
| Уравнение притока к скважине | 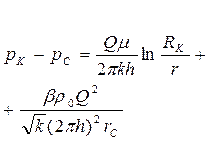 (100)
(100)
| 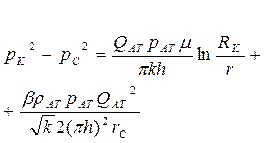 (101)
(101)
|
Из (100) и (101) видно, что индикаторная линия, построенная в координатах для жидкости и 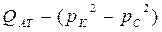 для газа, является параболой (Рис. 8, 9).
для газа, является параболой (Рис. 8, 9).
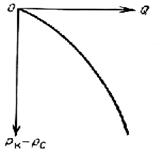 | 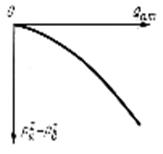 | ||
Рис. 8. Индикаторная линия Рис. 9. Индикаторная линия
при фильтрации жидкости при фильтрации газа по
по двучленному закону. двучленному закону.
Уравнение притока к скважине для несжимаемой жидкости имеет вид:
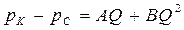 (102)
(102)
для газа
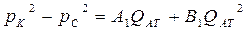 (103)
(103)
где
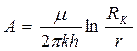
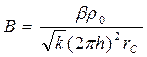 (104)
(104)
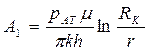
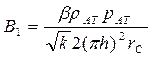 (105)
(105)
А, В, А1, В1, - коэффициенты фильтрационного сопротивления, являются постоянными для данной скважины.
Скважины исследуют на 5 – 6 режимах (однако ка показывают исследования и результаты обработки индикаторных линий этих замеров недостаточно, необходимо увеличить число замеров для более точного определения коэффициентов фильтрационного сопротивления. Кроме того можно упомянуть об аномальных видах индикаторной линии, о случаях кольматации и наоборот раскольматирования при высоких отборах).
Затем скважину закрывают и давление на забое остановленной скважины принимают за контурное давление рк.
Уравнения (102) и (103) можно представить соответственно к уравнению прямой:
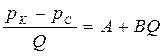 (106)
(106)
 |
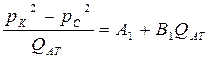 (107)
(107)
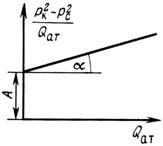
Рис. 10. График зависимости 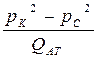 от
от 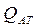 при фильтрации газа по двучленному закону
при фильтрации газа по двучленному закону
Коэффициент А – отрезок, отсекаемый на оси ординат, В – тангенс угла наклона прямой к оси абсцисс. (Рис. 10).
По значениям коэффициентов А и В определяют коллекторские свойства пласта: коэффициент проницаемости (эффективный), эффективную мощность пласта, коэффициент гидропроводности:
Для нефтяной скважины
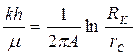 (108)
(108)
Для газовой скважины
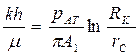 (109)
(109)
Дата добавления: 2015-11-10; просмотров: 3577;
