Адиабатический процесс. Уравнение Пуассона.

а) Процесс, протекающий в термодинамической системе без теплообмена с окружающей средой, называется адиабатическим (адиабатным). Для практического осуществления такого процесса газ помещают в сосуд с теплоизоляционными стенками. Поскольку любой материал в той или иной степени проводит теплоту, то процесс можно считать адиабатическим лишь приближённо. Хорошим приближением к адиабатическому процессу являются быстро протекающие процессы. Кратковременность процесса приводит к тому, что система не успевает обменяться теплотой с окружающей средой. При адиабатическом процессе газ не отдаёт и не получает количество теплоты, т.е. dQ = 0. Тогда первый закон термодинамики имеет вид:

0 = dU + dA или dA = – dU , (23)

т.е. работа, совершаемая газом при адиабатическом процессе, производится только за счёт изменения его внутренней энергии. Если газ расширяется, то dV > 0 и dA = P·dV > 0. Из формул (23) следует, что dU < 0, а следовательно, температура газа понижается. Если же газ сжимается, то dA < 0 и dU > 0, а его температура повышается. Этим объясняется, например, нагревание воздуха в цилиндре дизельного двигателя при его сжатии.

б) Уравнение, которое описывает адиабатический процесс, происходящий в газе, таково:

PV ^g = const, (24)

Изотерма Адиабата 0 V P Рис. 2

где P — давление газа, V — объём, занимаемый газом, g = C_mP / C_mV — отношение молярных теплоёмкостей при изобарическом и изохорическом процессах. Это соотношение называется уравнением Пуассона. Уравнение Пуассона можно записать в ином виде, воспользовавшись уравнением Менделеева — Клапейрона. Из него находим, что 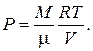Подставляя это выражение в (24) и учитывая, что величины M, m и R постоянные, получаем:

TV ^g–1 = const. (25)

Используя выражения (19) и (20), находим: 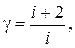где i — число степеней свободы молекулы. График, соответствующий уравнению Пуассона, называется адиабатой (рис. 2). Поскольку всегда g > 1, то адиабата идёт круче изотермы, соответствующей закону Бойля — Мариотта.