ВИДЫ РАВНОВЕСИЯ
В статике абсолютно твёрдого тела различают три вида равновесия.
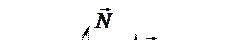 1. Рассмотрим шарик, который находится на вогнутой поверхности. В положении, показанном на рис. 88, шарик находится в равновесии: сила реакции опоры
1. Рассмотрим шарик, который находится на вогнутой поверхности. В положении, показанном на рис. 88, шарик находится в равновесии: сила реакции опоры 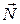 уравновешивает силу тяжести
уравновешивает силу тяжести 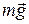 .
.
Если отклонить шарик от положения равновесия, то векторная сумма сил тяжести и реакции опоры уже не равна нулю: возникает сила 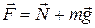 , которая стремится вернуть шарик в первоначальное положение равновесия (в точку О).
, которая стремится вернуть шарик в первоначальное положение равновесия (в точку О).
Это пример устойчивого равновесия.
У с т о й ч и в ы м называется такой вид равновесия, при выходе из которого возникают силы или моменты сил, которые стремятся вернуть тело в положение равновесия.
Потенциальная энергия шарика в любой точке вогнутой поверхности больше, чем потенциальная энергия в положении равновесия (в точке О). Например, в точке А (рис. 88) потенциальная энергия больше, чем потенциальная энергия в точке О на величину Еп(А) - Еп(0) = mgh.
В положении устойчивого равновесия потенци- альная энергия тела имеет минимальное значение по сравнению с соседними положениями.
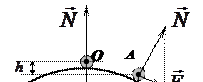 2. Шарик на выпуклой поверхности находится в положении равновесия в верхней точке (рис. 89), где сила тяжести
2. Шарик на выпуклой поверхности находится в положении равновесия в верхней точке (рис. 89), где сила тяжести 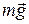 уравновешена силой реакции опоры
уравновешена силой реакции опоры 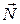 . Если отклонить шарик от точки О, то возникает сила
. Если отклонить шарик от точки О, то возникает сила 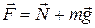 , направленная в сторону от положения равновесия.
, направленная в сторону от положения равновесия.
Под действием силы 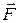 шарик будет удаляться от точки О. Это пример неустойчивого равновесия.
шарик будет удаляться от точки О. Это пример неустойчивого равновесия.
Н е у с т о й ч и в ы м называется такой вид равновесия, при выходе из которого возникают силы или моменты сил, которые стремятся увести тело ещё дальше от положения равновесия.
Потенциальная энергия шарика на выпуклой поверхности имеет наибольшее значение (максимум) в точке О. В любой другой точке потенциальная энергия шарика меньше. Например, в точке А (рис. 89) потенциальная энергия меньше, чем в точке О, на величину Еп(0) - Еп(А) = mgh.
 В положении неустойчивого равновесия потен-циальная энергия тела имеет максимальное значение по сравнению с соседними положениями.
В положении неустойчивого равновесия потен-циальная энергия тела имеет максимальное значение по сравнению с соседними положениями.
3. На горизонтальной поверхности силы, действующие на шарик, уравновешены в любой точке: 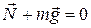 (рис. 90). Если, например, сместить шарик из точки О в точку А, то равнодействующая сил
(рис. 90). Если, например, сместить шарик из точки О в точку А, то равнодействующая сил
тяжести и реакции опоры по-прежнему равна нулю, т.е. в точке А шарик также находится в положении равновесия.
Это пример безразличного равновесия.
Б е з р а з л и ч н ы м называется такой вид равновесия, при выходе из которого тело остаётся в новом положении в равновесии.
Потенциальная энергия шарика во всех точках горизонтальной поверхности (рис. 90) одинакова.
В положениях безразличного равновесия потен- циальная энергия одинакова.
Иногда на практике приходится определять вид равновесия тел различной формы в поле сил тяжести. Для этого нужно запомнить следующие правила:
1. Тело может находиться в положении устой- чивого равновесия, если точка приложения силы реакции опоры находится выше центра тяжести тела. При этом эти точки лежат на одной вертикали (рис. 91).
 На рис. 91, б роль силы реакции опоры играет сила натяжения нити
На рис. 91, б роль силы реакции опоры играет сила натяжения нити 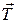 .
.
2. Когда точка приложения силы реакции опоры находится ниже центра тяжести, возможны два случая:
— если опора точечная (площадь поверхности опоры мала), то равновесие неустойчивое (рис. 92). При небольшом отклонении от положения равновесия момент сил 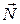 и
и 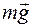 стремится увеличить отклонение от начального положения;
стремится увеличить отклонение от начального положения;
 — если опора неточечная (площадь поверх- ности опоры велика), то положение равновесия устой- чивое в том случае, когда линия действия силы тяжести АА' пересекает поверхность опоры тела
— если опора неточечная (площадь поверх- ности опоры велика), то положение равновесия устой- чивое в том случае, когда линия действия силы тяжести АА' пересекает поверхность опоры тела
(рис. 93). В этом случае при небольшом отклонении тела от положения равновесия возникает момент сил 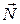 и
и 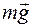 , который возвращает тело в первоначальное положение.
, который возвращает тело в первоначальное положение.

??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Как изменяется положение центра тяжести тела, если тело вывести из положения: а) устойчивого равновесия? б) неустойчивого равновесия?
2. Как изменяется потенциальная энергия тела, если изменить его положение при безразличном равновесии?
| устойчивое равновесие | stable equilibrium | équilibre stable | equilibrio estable |
| неустойчивое равновесие | unstable equilibrium | équilibre instable | equilibrio inestable |
| безразличное равновесие | neutral equilibrium | quilibre indifférent | equilibrio indiferente |
| минимум | minimum | minimum | mínimo |
| максимум | maximum | maximum | máximo |
| сместить | displace | éсarter | desplazar |
Основные формулы статики
Момент силы
M = F× d
Общее условие равновесия:
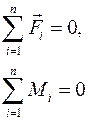 Координаты центра тяжести системы тел:
Координаты центра тяжести системы тел:
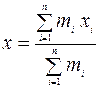 ; ; 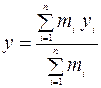 ; ; 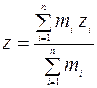 Момент пары сил
M = F× ℓ
Момент пары сил
M = F× ℓ
|
Дата добавления: 2015-09-28; просмотров: 1855;
