Кинетическая энергия. К и н е т и ч е с к а я э н е р г и я — это энергия движения: она зависит от скорости и массы тела:
К и н е т и ч е с к а я э н е р г и я — это энергия движения: она зависит от скорости и массы тела:
Ек = Ек (υ).
Пусть в состоянии 1 тело покоится в данной системе отсчёта; при этом его скорость равна нулю и в этом состоянии кинетическая энергия равна нулю Ек = 0. Под действием постоянной силы 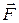 тело движется прямолинейно и равноускоренно и переходит в состояние 2. При этом его скорость изменяется от нуля до
тело движется прямолинейно и равноускоренно и переходит в состояние 2. При этом его скорость изменяется от нуля до 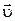 на перемещении
на перемещении 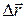 (рис. 75). Внешняя сила
(рис. 75). Внешняя сила 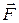 на перемещении
на перемещении 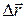 совершает работу
совершает работу

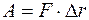 , так как
, так как 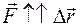 . В состоянии 2 шар получает запас кинетической энергии
. В состоянии 2 шар получает запас кинетической энергии
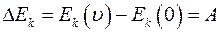 ,
,
но так как 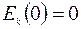 , то
, то
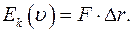 (III.9)
(III.9)
По второму закону Ньютона F = m×a; по формуле кинематики для равноускоренного движения
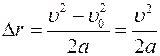 , (υ0) = 0.
, (υ0) = 0.
Подставим выражение модуля силы и модуля перемещения в формулу (III.9) и получим формулу кинетической энергии
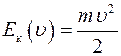 .
.
Кинетическая энергия тела равна половине произведения массы тела на квадрат скорости тела.
Если движущееся тело совершает работу А, то его кинетическая энергия уменьшается:
ΔЕк = - А < 0.
4.3. Законы сохранения и изменения механической энергии
Полная механическая энергия есть сумма потенциальной и кинетической энергии тела (системы тел), которыми тело (система тел) обладают одновременно:
Е = Еп + Ек.
Рассмотрим, как изменяется полная механическая энергия тела массы т при движении по наклонной плоскости высотой h и длиной ℓ.
Пусть в систему тел входят тело массы т, наклон- ная плоскость (опора) и Земля. При взаимодействии системы тел перемещения Земли и опоры и изменение их скорости очень малы. Значит, изменения механичес- кой энергии Земли и опоры тоже очень малы и их мож- но не учитывать. Внешние силы на систему тел не действуют, следовательно, система изолированная.

С л у ч а й 1. В системе тел нет неконсервативных сил: нет трения между телом и поверхностью опоры (рис. 76).
В начальный момент времени тело находится в состоянии 1:
— на высоте h над уровнем Земли потенциальная энергия тела Еп (1) = mgh;
— начальная скорость тела равна нулю; кинети- ческая энергия тела Ек(1) = 0.
Полная механическая энергия тела в состоянии 1
E(l) = Eп(l) + Eк(l) = mgh. (III.10)
В конечный момент времени тело находится в состоянии 2:
— на уровне земли потенциальная энергия тела Еп (2) = 0;
— скорость тела равна 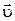 ; кинетическая энергия
; кинетическая энергия
 .
.
Полная механическая энергия тела в состоянии 2
 . (III.11)
. (III.11)
Преобразуем формулу (III.1). Из проекции уравнения второго закона Ньютона на ось 0Х, которую мы выбираем параллельно наклонной плоскости,
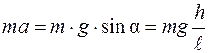 (III.12)
(III.12)
следует, что под действием постоянной силы mg 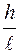 тело движется с постоянным ускорением
тело движется с постоянным ускорением 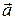 . Из формулы кинематики для равноускоренного движения
. Из формулы кинематики для равноускоренного движения 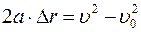 , где в данном случае модуль переме- щения Δr = ℓ, υ0 = 0, находим формулу ускорения
, где в данном случае модуль переме- щения Δr = ℓ, υ0 = 0, находим формулу ускорения 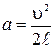 , которую подставляем в формулу (III.12):
, которую подставляем в формулу (III.12):
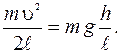
Из последнего равенства следует
 (III.13)
(III.13)
Сравнивая формулы (III.10) и (III.13), мы видим, что в данном случае потенциальная энергия тела переходит в кинетическую энергию, но полная механическая энергия тела не изменяется (сохраняется).
Сформулируем закон сохранения механической энергии.
Полная механическая энергия изоли- рованной системы тел есть величина посто- янная при отсутствии внутренних некон- сервативных сил.
С л у ч а й 2. В системе тел действуют неконсер- вативные силы: между телом и поверхностью опоры есть трение (рис. 77).

В состоянии 1 (на вершине наклонной плоскости) полная механическая энергия тела равна потенциаль- ной энергии
Е(1) = тgh.
В состоянии 2 (на уровне поверхности Земли) полная энергия тела равна кинетической энергии
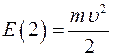 .
.
Найдём выражение Е(2)как функции h и ℓ в этом cлучае.
Подставим кинематическую формулу ускорения  в формулу второго закона Ньютона, записанную в скалярном виде в проекции на ось ОХ (рис. 77)
в формулу второго закона Ньютона, записанную в скалярном виде в проекции на ось ОХ (рис. 77)  - Fтр.
- Fтр.
В результате получим Е(2) = 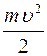 = mgh - Fтp× ℓ,
= mgh - Fтp× ℓ,
или Е(2) = Е(1)+Атр. (III.14)
где Атр. = -Fтp.× ℓ — работа силы трения.
Из формулы (III. 14) видно, что в данном случае полная энергия изолированной системы тел не сохраняется: часть ее расходуется на работу против неконсервативной силы (силы трения).
В том случае, когда система тел неизолированная, часть ее полной механической энергии расходуется на работу против внешних сил.
Сформулируем закон изменения полной механической энергии.
Изменение полной механической энергии изолированной системы тел равно работе неконсервативных сил (сил трения)
ΔЕизолир. = Атр.
Изменение полной механической энергии неизолированной системы тел равно работе всех внутренних неконсервативных сил и работе внешних сил:
ΔЕнеизолир. = åАвнеш.+ åАвнутр. неконс.
Законы сохранения и изменения механической энергии являются частными случаями фундамен- тального закона природы — закона сохранения энергии. Физические тела могут иметь запас не только механической энергии, но и других видов энергии: тепловой, электрической, ядерной. Фундаментальный закон сохранения энергии утверждает, что энергия физических тел не создаётся и не исчезает, она превращается из одного вида в другой или передаётся от одного тела к другому в равных количествах.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Зависит ли кинетическая энергия тела от направле- ния его скорости?
2. Тело движется равномерно. Может ли его кинети- ческая энергия быть больше кинетической энергии тела, которое движется равноускоренно?
3. Выполняется ли закон сохранения или закон изменения энергии для тела, брошенного вертикально вверх?
4. Какие виды энергии вы знаете?
| создаваться | be created | se former | crear |
| исчезать | disappear | disparаître | desaparecer |
| Основные формулы механической работы и энергии | |
Работа постоянной силы
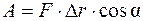 Работа силы тяжести
А = mg (h2 – h 1)
Работа силы упругости
Работа силы тяжести
А = mg (h2 – h 1)
Работа силы упругости
 Мощность
Мощность
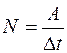
| Коэффициент полезного
действия
 Полная энергия
Е = Еп + Ек
Потенциальная энергия:
силы тяжести Еп = mgh
силы упругости
Полная энергия
Е = Еп + Ек
Потенциальная энергия:
силы тяжести Еп = mgh
силы упругости 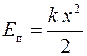 Кинетическая энергия
Кинетическая энергия
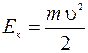
|
| Закон сохранения энергии (для изолированной системы тел без трени): ΔЕизолир. = 0 Закон изменения энергии: для изолированной системы тел с трением ΔЕизолир. = А тр. для неизолированной системы тел ΔЕнеизолир. = SА внеш. + åАвнутр. неконс. |
IV. СТАТИКА
С т а т и к а — это часть механики, которая изучает условия равновесия тела или системы тел.
Будем считать, что тело находится в равновесии, если оно находится в состоянии покоя в инерциальной системе отсчёта.
Если в динамике мы рассматривали физическое тело как материальную точку, то при изучении равно- весия тела его формой и размерами пренебречь нельзя. В статике используют модель физического тела — абсолютно твёрдое тело.
А б с о л ю т н о т в ё р д о е т е л о ¾ это система материальных точек, расстояния между которыми не меняются в процессе движения. Реальное тело можно считать абсолютно твёрдым телом, если в условиях рассматриваемой задачи его деформации пренебрежимо малы.
Абсолютно твёрдое тело может двигаться поступательно и вращательно.
При п о с т у п а т е л ь н о м д в и ж е н и и отрезок прямой линии, соединяющий две любые точки твёрдого тела, остаётся параллельным самому себе.
При в р а щ а т е л ь н о м д в и ж е н и и тела вокруг неподвижной оси все точки твёрдого тела движутся по окружностям, центры которых лежат на одной прямой линии, которая называется осью вращения.
1. СТАТИКА ТЕЛА,
НЕ ИМЕЮЩЕГО НЕПОДВИЖНОЙ ОСИ ВРАЩЕНИЯ
Тело, которое не имеет неподвижной оси вращения, может двигаться поступательно и одновременно вращаться вокруг некоторой оси.. Если такое тело находится в равновесии, т. е. находится в состоянии покоя или равномерного прямолинейного движения, то его ускорение равно нулю. Тогда по второму закону Ньютона векторная сумма всех сил, действующих на тело, равна нулю, т.е. на тело действуют уравновешенные силы или не действуют никакие силы.

Рис. 78
Сформулируем условие отсутствия поступатель- ного движения тела, не имеющего неподвижной оси вращения.
Тело, не имеющее неподвижной оси вращения, не движется поступательно, если векторная сумма действующих на него сил равна нулю.
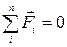 . (Ⅳ.1)
. (Ⅳ.1)
(на рис. 78, а ,б n = 3, т. е. 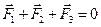 )
)
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Какое тело можно считать абсолютно твердым те- лом?
2. Как формулируется условие отсутствия поступа- тельного движения тела, не имеющего неподвижной оси вращения?
| статика | statics | statique | stática |
| равновесие | equilibrium | équilibre | equilibrio |
| твердое тело | solid body | corps solide | cuerpo sólido |
| ось вращения | axis of rotation | axe de rotation | eje de rotación |
2. СТАТИКА ТЕЛА,
ИМЕЮЩЕГО НЕПОДВИЖНУЮ ОСЬ ВРАЩЕНИЯ
Если тело имеет неподвижную ось вращения, то под действием внешних сил оно может совершать только вращательное движение.
 Рассмотрим диск, который может свободно (без трения) вращаться вокруг неподвижной оси О¢О² (рис. 79). Пусть в точке А на диск действует сила
Рассмотрим диск, который может свободно (без трения) вращаться вокруг неподвижной оси О¢О² (рис. 79). Пусть в точке А на диск действует сила 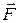 . Сила
. Сила 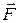 лежит в плоскости, перпендикулярной оси (рис. 80). Разложим вектор этой силы на два составляющих вектора:
лежит в плоскости, перпендикулярной оси (рис. 80). Разложим вектор этой силы на два составляющих вектора: 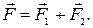 Сила
Сила 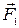 направлена вдоль радиуса, прохо- дящего через точку А. Эта сила уравновешена силой реакции опоры неподвижной оси
направлена вдоль радиуса, прохо- дящего через точку А. Эта сила уравновешена силой реакции опоры неподвижной оси 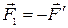 . Она не вызывает движения диска. Сила
. Она не вызывает движения диска. Сила 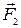 направлена перпендикулярно радиусу, проведённому через точку приложения силы
направлена перпендикулярно радиусу, проведённому через точку приложения силы 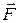 : ОА
: ОА 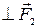 , т. е. отрезок прямой ОА есть кратчайшее расстояние от оси вращения (точки О) до линии действия силы
, т. е. отрезок прямой ОА есть кратчайшее расстояние от оси вращения (точки О) до линии действия силы 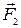 . Сила
. Сила 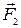 не уравнове- шена никакой другой силой: она вызывает вращательное движение диска. Мы видим, что условия равновесия или движения тела здесь зависят от двух факторов: модуля силы и кратчайшего расстояния от оси вращения до линии действия силы. Поэтому в статике тел, имеющих неподвижную ось вращения, вводится понятие момента силы.
не уравнове- шена никакой другой силой: она вызывает вращательное движение диска. Мы видим, что условия равновесия или движения тела здесь зависят от двух факторов: модуля силы и кратчайшего расстояния от оси вращения до линии действия силы. Поэтому в статике тел, имеющих неподвижную ось вращения, вводится понятие момента силы.
 М о м е н т с и л ы
М о м е н т с и л ы 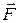 относительно оси, проходящей через точку О, ¾ это физическая величина, модуль которой равен произведению модуля силы на кратчайшее расстояние d от точки О до линии действия силы:
относительно оси, проходящей через точку О, ¾ это физическая величина, модуль которой равен произведению модуля силы на кратчайшее расстояние d от точки О до линии действия силы:
M = F× d. (IV.2)
Мы будем рассматривать момент силы как скалярную величину, которая может быть положительной и отрицательной.
Будем считать, что если сила стремится вращать тело против часовой стрелки относительно оси, проходящей через точку О, то момент силы — положительный (имеет знак плюс).
Тогда момент силы, которая стремится вращать тело по часовой стрелке относительно оси, проходящей через точку О, — отрицательный (имеет знак минус).
Кратчайшее расстояние от оси, проходящей через точку О, до линии действия силы называется п л е ч о м э т о й с и л ы ¾ d.
Модуль момента силы относительно данной оси равен произведению модуля силы на плечо этой силы (формула (IV.2)).
 В примере, рассмотренном на рис. 80, сила
В примере, рассмотренном на рис. 80, сила 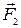 , которая вызывает вращение диска, имеет плечо d = ОA и стремится вращать диск по часовой стрелке.
, которая вызывает вращение диска, имеет плечо d = ОA и стремится вращать диск по часовой стрелке.
В данном примере момент силы 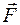 равен моменту силы
равен моменту силы 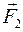 , т. к.
, т. к.  и
и  (смотри рис. 81).
(смотри рис. 81).
Момент силы 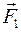 равен нулю, т.к. плечо силы равно нулю.
равен нулю, т.к. плечо силы равно нулю.
Единицы момента силы в СИ:
[М] = [F]×[d] = 1 Н××м = 1 кг× м2/с2.
Единица момента силы в системе СГС:
[М] = 1 дин × см = 1 г × см2/с2.
 Рассмотрим тело, имеющее неподвижную ось вращения, которая проходит через точку О (рис. 82). Пусть на это тело в точках А и В действуют две силы: сила
Рассмотрим тело, имеющее неподвижную ось вращения, которая проходит через точку О (рис. 82). Пусть на это тело в точках А и В действуют две силы: сила 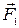 , которая стремится вращать тело против часовой стрелки, и сила
, которая стремится вращать тело против часовой стрелки, и сила 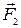 , которая стремится вращать тело по часовой стрелке. Силы
, которая стремится вращать тело по часовой стрелке. Силы 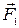 и
и 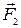 лежат в плоскости, перпендикулярной оси вращения. Моменты этих сил равны соответственно
лежат в плоскости, перпендикулярной оси вращения. Моменты этих сил равны соответственно
M1 = F1× d1 , M2 = - F2 × d2.
Опыт показывает, что, если алгебраическая сумма моментов М1и М2больше нуля (M1 + M2 > 0), то тело будет поворачиваться против часовой стрелки.
Если алгебраическая сумма моментов М1и М2меньше нуля (M1 + M2 < 0), то тело будет поворачиватья по часовой стрелке.
Значит, можно сделать вывод:
тело находится в равновесии, если алгебраическая
сумма моментов М1и М2 равна нулю.
Если на тело действуют несколько сил, то это правило остается верным, т.е. мы можем сформулировать условие равновесия тела, имеющего неподвижную ось вращения — правило моментов:
тело, имеющее неподвижную ось вращения, нахо-
дится в равновесии, если алгебраическая сумма
моментов всех сил, действующих на него, равна нулю.
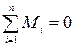 . (IV.3)
. (IV.3)
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. От каких факторов зависит равновесие или движе- ние тела, имеющего ось вращения?
2. Какой момент силы считается положительным?
3. При каком условии тело, имеющее ось вращения, находится в равновесии?
| вращательное движение | rotational motion | movement de rotation | movimiento de rotación |
| диск | disk | disque | disco |
| кратчайший | the shortest | le plus court | minimo |
| момент силы | moment of force | moment dˋune force | momento de fuerza |
| плечо силы | arm of force | bras de force | brazo de la fuerza |
| по часовой стрелке | clockwisПe | dans le sens des aiguilles dˋune montre | en el sentido de las manecillas |
| против часовой стрелки | counterclock- wise | dans le sens inverse des aiguilles dˋune montre | del reloj de derecha a la izquierda |
3. ОБЩЕЕ УСЛОВИЕ РАВНОВЕСИЯ ТЕЛА
В общем случае абсолютно твёрдое тело может совершать одновременно два движения: поступатель- ное и вращательное.
При этом, чтобы тело находилось в равновесии, должны выполняться сразу два условия равновесия (IV. 1) и (IV. 3). Так как тело, которое может двигаться и поступательно, и вращательно, не имеет неподвижной оси вращения, то момент сил, действующих на такое тело, можно определить относительно любой оси, проходящей через любую точку.
Сформулируем общее условие равновесия.
Тело находится в равновесии, если векторная сумма всех действующих на него сил равна нулю и алгебраическая сумма моментов всех сил относительно любой оси равна нулю:
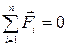 , (IV.4a)
, (IV.4a)
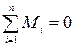 . (IV.4б)
. (IV.4б)
Общее условие равновесия (IV.4) можно использовать для расчёта любых статических систем абсолютно твёрдых тел.
4. РАВНОВЕСИЕ ТЕЛА ПОД ДЕЙСТВИЕМ ПАРАЛЛЕЛЬНЫХ СИЛ
На практике часто встречается случай, когда к телу одновременно приложены несколько сил, линии действия которых параллельны. Такие силы называются п а р а л л е л ь н ы м и с и л а м и.
Задача о сложении параллельных сил состоит в том, чтобы найти величину, направление и точку приложения равнодействующей силы.
Рассмотрим пример.

На абсолютно твёрдый горизонтальный стержень ОО'действуют силы 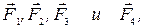 как показано на рис. 83. Расстояния ОА, ОВ, ОС и ОD считаем известными. Стержень будет находиться в равновесии, если в некоторой точке X к нему приложить силу
как показано на рис. 83. Расстояния ОА, ОВ, ОС и ОD считаем известными. Стержень будет находиться в равновесии, если в некоторой точке X к нему приложить силу 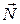 , равную по модулю и противоположную по направле- нию равнодействующей силе
, равную по модулю и противоположную по направле- нию равнодействующей силе
 . Найдём модуль R = N и направление равнодействующей силы и расстояние ОХ от начала координат до точки ее приложения. Для решения задачи используем общее условие равновесия (IV.4). При этом уравнение (IV.4а)
. Найдём модуль R = N и направление равнодействующей силы и расстояние ОХ от начала координат до точки ее приложения. Для решения задачи используем общее условие равновесия (IV.4). При этом уравнение (IV.4а)
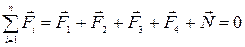
записываем в проекциях на ось ОУ;
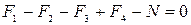 ,
,
откуда находим величину равнодействующей силы
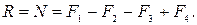
Если при подстановке численных значений результат имеет знак плюс, то сила R направлена так, как показано на рис. 83; если результат имеет знак минус, то сила R направлена в противоположную сторону. Таким образом, мы нашли модуль и направление равнодействующей силы. Точку её приложения найдём из уравнения (IV. 4б).
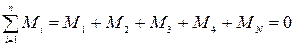 .
.
Моменты сил можно определять относительно любой точки. В данном случае удобно вычислить моменты сил относительно точки О:
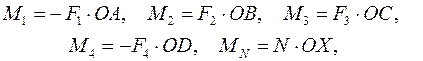
где неизвестно только расстояние ОХ. Подставляя значения моментов в последнее уравнение, находим
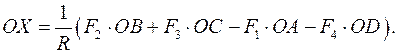
Задача о равновесии стержня под действием параллельных сил решена.
|
 Пусть на тело действует пара сил, равных по величине F
Пусть на тело действует пара сил, равных по величине F 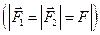 . Расстояние между линиями действия сил АВ = ℓ (рис. 84) называется плечом пары сил. Найдём суммарный момент пары сил относительно оси, проходящей через произвольную точку О:
. Расстояние между линиями действия сил АВ = ℓ (рис. 84) называется плечом пары сил. Найдём суммарный момент пары сил относительно оси, проходящей через произвольную точку О:
M = M1+ M 2 = F× (AО + ОB)=F× ℓ.
Момент пары сил относительно оси, проходящей через произвольную точку, есть произведение модуля одной силы на плечо пары
M=F× ℓ.
Дата добавления: 2015-09-28; просмотров: 1275;
