ДИНАМИКА СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Как будет показано далее (стр. 117), система тел совершает свободные гармонические колебания, если в ней действует внутренняя сила, всегда направленная в сторону положения устойчивого равновесия и по величине прямо пропорциональная смещению
Fх = - l×x. (VI.3)
В формуле (VI.3) множитель l — это коэффициент пропорциональности, а знак минус указывает на то, что сила 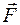 направлена в сторону положения равновесия, т.е. противоположно направлению смещения х. Силу
направлена в сторону положения равновесия, т.е. противоположно направлению смещения х. Силу 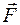 иногда называют в о з в р а щ а ю щ е й с и л о й.
иногда называют в о з в р а щ а ю щ е й с и л о й.
Покажем, что силы типа (VI.3) действуют в колебательных системах, которые называются м а т е м а т и ч е с к и м м а я т н и к о м и п р у ж и н н ы м м а я т н и о м. Исследуем динамику свободных гармонических колебаний на примере этих механических колебательных систем.
 Математический маятник (рис. 104) состоит из тела массы т, подвешенного на нерастяжимой нити длиной АВ = ℓ в поле сил тяжести. При этом тело, которое считается материальной точкой, может отклоняться от положения равновесия О на малый угол α. В точке В на тело действуют сила тяжести
Математический маятник (рис. 104) состоит из тела массы т, подвешенного на нерастяжимой нити длиной АВ = ℓ в поле сил тяжести. При этом тело, которое считается материальной точкой, может отклоняться от положения равновесия О на малый угол α. В точке В на тело действуют сила тяжести 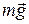 и сила натяжения нити
и сила натяжения нити 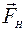 .
.
 Проекция равнодействующей силы
Проекция равнодействующей силы 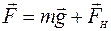 на направление смещения равна Fх = - mg×sinα, но так как угол α мал, то sinα » α и Fх = - mg×α. Величина угла α в радианной мере есть отношение длины дуги ОВ (которая приближенно равна смещению х) к длине нити ℓ :
на направление смещения равна Fх = - mg×sinα, но так как угол α мал, то sinα » α и Fх = - mg×α. Величина угла α в радианной мере есть отношение длины дуги ОВ (которая приближенно равна смещению х) к длине нити ℓ : 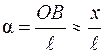 .
.
Следовательно, в случае математического маятника выражение для возвращающей силы имеет вид (VI.3) при 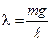 :
:
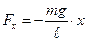 . (VI.4)
. (VI.4)
Динамика движения математического маятника подчиняется второму закону Ньютона, уравнение которого мы запишем в проекции на ось ОХ:
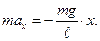
Сократим в этом уравнении массу и, обозначая
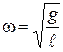 , (VI.5)
, (VI.5)
получаем уравнение движения математического маятника
ах = - w2× х.(VI.6)
Решение уравнения (VI.3), которое можно найти, используя высшую математику, имеет вид (VI. 1)
х (t) = А × sin (wt + j0).
Значения амплитуды А и начальной фазы j0 определяются начальными условиями: величиной смещения (VI. 1) и скорости (VI.2) движения маятника в начальный момент времени:
x0 = x(t = 0), υ0 = υ (t = 0).
Начальные условия можно задавать произвольно.
Период колебаний математического маятника Т связан с циклической частотой w соотношением Т = 2p/w; подставляя в это соотношение значение циклической частоты из формулы (VI.5), находим
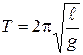 . (VI.7)
. (VI.7)
 Период колебаний математического маятника не зависит от массы тела. Период тем больше, чем больше длина нити маятника.
Период колебаний математического маятника не зависит от массы тела. Период тем больше, чем больше длина нити маятника.
Математический маятник можно использовать для приближенного вычисления величины ускорения свободного падения. Для этого нужно экспериментально измерить длину нити ℓ и период колебаний маятника Т, после чего из формулы (VI.7) определяется модуль ускорения свободного падения
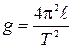 . (VI.8)
. (VI.8)
Пружинный маятник (рис. 105) состоит из тела массой т — груза, который может перемещаться без трения по горизонтальной оси под действием силы упругости пружины с коэффициентом упругости k. Положение груза в точке 0, когда пружина не растянута и не сжата, — это положение равновесия. Если сместить груз вправо (растянуть пружину) и отпустить его, то груз под действием силы 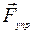 со стороны пружины будет совершать колебательное движение около положения равновесия. Проекция на ОХ силы, действующей на груз, по закону Гука равна Fх = - k×x. Возвращающая сила имеет вид (VI.3) при l = k. Значит, колебания пружинного маятника будут гармоническими.
со стороны пружины будет совершать колебательное движение около положения равновесия. Проекция на ОХ силы, действующей на груз, по закону Гука равна Fх = - k×x. Возвращающая сила имеет вид (VI.3) при l = k. Значит, колебания пружинного маятника будут гармоническими.
Из уравнения второго закона Ньютона, записанного
в проекции на ось ОХ: тах = - k× x, следует уравнение
колебаний пружинного маятника
ах = - w2 × х, (VI.9)
в котором мы сделали обозначение
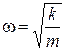 . (VI.10)
. (VI.10)
Сравнивая уравнения движения пружинного маятника (VI.9) и математического маятника (VI.6), мы видим, что эти уравнения точно совпадают. Значит, совпадают и решения этих уравнений: зависимость смещения груза от времени также описывается формулой (VI.1)
х (t) = А × sin (wt + j0).
Период колебаний находим по формуле Т = 2p/w, или
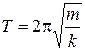 . (VI.11)
. (VI.11)
Период колебаний пружинного маятника тем больше, чем больше масса груза и чем меньше коэффициент упругости пружины.
Скорость 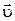 и ускорение тела
и ускорение тела 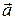 — это соответственно первая и вторая производные по времени радиуса вектора
— это соответственно первая и вторая производные по времени радиуса вектора 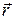 этого тела в некоторой системе координат
этого тела в некоторой системе координат
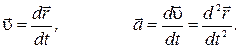
Возьмём проекции этих векторов на ось ОХ, так как и математический и пружинный маятники совершают колебательное движение вдоль оси ОХ. Проекция радиуса-вектора — это координата х, проекция скорости и ускорения
 .
.
Подставляя ускорение в формулу (VI.6) или (VI.9),
получаем дифференциальное уравнение
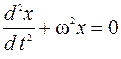 . (VI.12)
. (VI.12)
Уравнение вида (VI. 12) называется уравнением гармонических колебаний.
Проверим, является ли функция (VI.1) х = А × sin (wt + j0) решением уравнения гармонических колебаний. Для этого два раза продифференцируем (VI. 1):
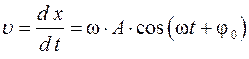 — это формула зависимости скорости от времени при гармонических колебаниях,
— это формула зависимости скорости от времени при гармонических колебаниях,
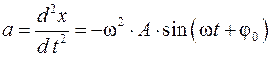 — это формула зависимости ускорения от времени при гармонических колебаниях.
— это формула зависимости ускорения от времени при гармонических колебаниях.
После подстановки смещения х и ускорения а в уравнение (VI.12) это уравнение становится тождеством, т.е. (VI.1) есть решение уравнения гармонических колебаний.
!!! Запомните формулы и соотношения
для гармонических колебаний:
смещение: х = А × sin (wt + j0)
скорость: υ = w× A ×cos (wt + j0)
ускорение: а = - w2×А × sin (wt + j0)
период колебаний:
— математического маятника
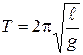 ;
— пружинного маятника ;
— пружинного маятника
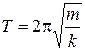 . .
|
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Под действием каких сил система тел может совершать свободные гармонические колебания?
2. Где больше период колебаний одного и того же математического маятника: на Земле или на Луне?
3. Если увеличить массу груза пружинного маятника, то частота его колебаний увеличится или уменьшится?
| возвращающая сила | returning force | force de rappel | fuerza regresiva |
| математический маятник | simple pendulum | pendule simple | péndulo simple |
| пружинный маятник | spring pendulum | pendule á réssort | péndulo de resоrte |
| начальные условия | initial conditions | conditions initiales | condiciones iniciales |
Дата добавления: 2015-09-28; просмотров: 1703;
