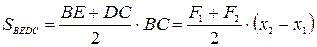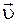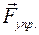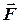НЕКОТОРЫЕ ДИНАМИЧЕСКИЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ
|
В результате этого взаимодействия:
— изменяются форма и объём тела, т. е. тело
деформируется (рис. 40, а),
— изменяется скорость (величина и направление),
т. е. тело получает ускорение (рис. 40, б).

а б
|
Вектор силы 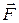 имеет три характеристики (рис. 41):
имеет три характеристики (рис. 41):
1) модуль F,
 2) направление (угол a),
2) направление (угол a),
3) точку приложения 0.
Точку приложения силы можно переносить по линии действия силы.
Если на тело действуют одновременно несколько сил, приложенных к одной точке, то мы можем их заменить одной силой, которая называется равнодействующей или результирующей силой 
Р а в н о д е й с т в у ю щ а я ( р е з у л ь т и р у- ю щ а я ) с и л а — это сила, действие которой заменяет одновременное действие нескольких сил.
Равнодействующая сила равна векторной сумме сил, действующих на тело.
На тело действуют две силы 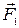 и
и  (рис. 42):
(рис. 42):
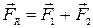 .
.
Равнодействующую силу можно найти по правилу сложения векторов.
 Если на тело действуют n сил, то равнодействующая сила равна векторной сумме этих сил:
Если на тело действуют n сил, то равнодействующая сила равна векторной сумме этих сил:
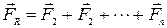 или
или 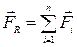 −
−
это сокращенная математическая запись:
символ  (читаем «сигма») означает сумму.
(читаем «сигма») означает сумму.
Если 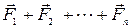 = 0, то силы
= 0, то силы 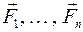 называются у р а в н о в е ш е н н ы м и с и л а м и.
называются у р а в н о в е ш е н н ы м и с и л а м и.
|
|
2. ЗАКОНЫ НЬЮТОНА
Основными законами динамики являются законы, открытые Исааком Ньютоном — великим английским учёным (1643—1727).
2.1. Первый закон Ньютона (закон инерции)
Тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют другие тела.
Системы отсчёта, в которых это условие выполняется, называютс инерциальными системами отсчета.
2.2. Второй закон Ньютона
В инерциальных системах отсчёта ускорение, которое получает тело под действием сил, прямо пропорционально равнодействующей силе:
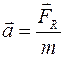 или
или  . (II.1)
. (II.1)
Из формулы (II.1) мы можем найти равнодействующую силу
 . (II.2)
. (II.2)
В формулах (II.1) и (II.2) m ¾ это коэффициент пропорциональности между ускорением и силой, который называется массой тела. Из (II.1) следует, что тело с бóльшей массой получает под действием данной силы мéньшее ускорение, то есть меньше изменяет свою скорость, следовательно, масса характеризует инертные свойства тела.
Масса тела ¾ это скалярная положительная физическая величина, которая количественно характеризует инертность тела.
Все тела в природе имеют массу. В механике Ньютона масса данного тела ¾ постоянная величина. Единица измерения массы в СИ ¾ 1 кг. Единица массы является основной единицей в СИ (смотри стр. 7).
Единица измерения силы в СИ называется ньютон(Н).
Используем формулу (II.2) для определения единицы силы [F] = [m] • [а]
Единица силы в СИ: 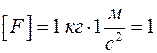 Н (ньютон).
Н (ньютон).
Единица силы в системе СГС: 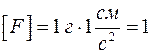 дин (дина).
дин (дина).
1 Н = 105 дин
Запишем выражение для ускорения
|
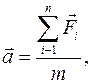 и
и
из определения ускорения 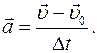
Приравняем правые части и получим равенство
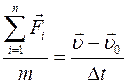 ,
,
откуда получим еще одну формулу второго закона Ньютона:
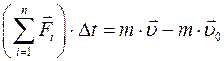 ,
,
где 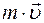 — импульс тела в момент времени t;
— импульс тела в момент времени t;  — импульс тела в момент времени t0.
— импульс тела в момент времени t0.
И м п у л ь с т е л а — это векторная физическая величина, равная произведению массы тела на его скорость.
Импульс тела и вектор скорости этого тела всегда имеют одинаковые направления: 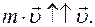
Величина ( 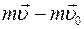 ) — это изменение импульса тела. Изменение импульса тела обозначается символом
) — это изменение импульса тела. Изменение импульса тела обозначается символом 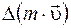 .
.
Величина  — это импульс силы.
— это импульс силы.
И м п у л ь с с и л ы — это векторная физическая величина, равная произведению силы на время действия силы.
Второй закон Ньютона в общем виде мы можем сформулировать так:
изменение импульса тела равно векторной сумме импульсов всех сил, действующх на тело:
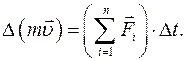
 2.3. Третий закон Ньютона
2.3. Третий закон Ньютона
Два тела действуют друг на друга с силами, которые:
— равны по модулю,
— направлены по одной прямой линии в
противоположные стороны,
— эти силы одной природы,
— эти силы приложены к разным телам
(рис. 43):
 .
.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. На тело действуют несколько сил. В каком
случае тело будет находиться в состояния покоя?
2. В каком случае импульс тела — постоянная величина?
3. Будут ли два тела с одинаковой массой иметь всегда одинаковые ускорения?
4. Имеют ли два тела с одинаковыми массами одинаковые импульсы?
5. Изменение импульса тела равно нулю, если скорость тела — постоянная величина. Правильно ли это?
| динамика | dynamics | dynamique | dinámica |
| сила | force | force | fuerza |
| действовать | act | agir | actuar |
| взаимодействие | interaction | intéraction | acción recíproca |
| деформация | deformation | déformation | deformación |
| инерция | inertia | inertie | inercia |
| импульс тела | momentum | impulsion | impulso |
| импульс силы | impuls of force | impulsion de force | impulso de la fuerza |
| точка приложения | application point | point dˋapplication | punto de aplicación |
| переносить | transport | transporter | transponer |
3. ВИДЫ СИЛ В МЕХАНИКЕ
Мы будем изучать три вида СИЛ: силы упругости, силы трения, силы гравитации.

3.1. Силы упругости
Под действием силы в теле возникают деформации.
Д е ф о р м а ц и я — это изменение формы или размеров тела.
Существует два вида деформации — упругая деформация и неупругая деформация.
При у п р у г о й д е ф о р м а ц и и форма и размеры тела после окончания действия силы, вызыва-
|

 ющей деформацию, такие же, как до начала действия силы (т. е. деформация исчезает после окончания действия силы).
ющей деформацию, такие же, как до начала действия силы (т. е. деформация исчезает после окончания действия силы).
На рис. 44 показаны два случая деформации:
—
|
— 




















|

 Английский учёный Р. Гук установил экспери- ментально, что величина абсолютной деформации тела прямо пропорциональна силе, вызывающей упругую деформацию: чем больше сила F, тем больше величина деформации ½Δх½:
Английский учёный Р. Гук установил экспери- ментально, что величина абсолютной деформации тела прямо пропорциональна силе, вызывающей упругую деформацию: чем больше сила F, тем больше величина деформации ½Δх½:




|
|
|

|






















 где
где 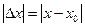 — абсолютная деформация (изменение длины пружины см. на рис. 45); k — коэффициент пропорциональности, который называется коэффициентом упругости или коэффициентом жёсткости пружины.
— абсолютная деформация (изменение длины пружины см. на рис. 45); k — коэффициент пропорциональности, который называется коэффициентом упругости или коэффициентом жёсткости пружины.



 Коэффициент упругости пружины зависит от:
Коэффициент упругости пружины зависит от:
|






 1) материала, из которого сделана пружина,
1) материала, из которого сделана пружина,
|
|
|





 2) размеров пружины.
2) размеров пружины.
|


 Единицы коэффициента упругости в СИ [k]=Н/м.
Единицы коэффициента упругости в СИ [k]=Н/м.
|
| |
|
 Прибор, который состоит из пружины и шкалы и
Прибор, который состоит из пружины и шкалы и
используется для измерения силы, называется
д и н а м о м е т р о м (рис. 46).
| |
| |
|
| |
| |
 В процессе упругой деформации в теле возникает сила упругости
В процессе упругой деформации в теле возникает сила упругости 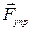 . Сила упругости стремится вернуть тело в начальное (недеформированное) положение. Сила упругости равна по модулю и противоположна по направлению деформирующей (внешней) силе
. Сила упругости стремится вернуть тело в начальное (недеформированное) положение. Сила упругости равна по модулю и противоположна по направлению деформирующей (внешней) силе 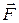 (см. рис. 45):
(см. рис. 45):
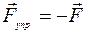
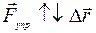 , поэтому
, поэтому
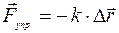 , или
, или 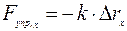 , или
, или
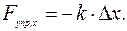
Последняя формула выражает закон Гука.
При упругой деформации сила упругости прямо пропорциональна абсолютной деформации тела и направлена в сторону, противоположную направлению перемещения точки приложения силы упругости.
Примеры сил упругости.
1) С и л а д а в л е н и я на опору 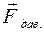 приложена к опоре и направлена перпендикулярно поверхности опоры.
приложена к опоре и направлена перпендикулярно поверхности опоры.
Сила давления вызывает деформацию опоры.
2) С и л а н о р м а л ь н о й реакции опоры 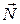 .
.
Тело, которое находится на опоре, деформирует опору.
Сила нормальной реакции опоры — это сила упругости, с которой деформированная опора действует на тело.
Сила нормальной реакции опоры 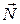 :
:
— приложена к телу,
— направлена нормально к поверхности опоры.
Из третьего закона Ньютона следует, что сила нормальной реакции и сила давления равны по модулю и противоположны по направлению. Эти силы приложены к разным телам (рис. 47): 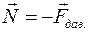 .
.

С и л а н а т я ж е н и я н и т и — это сила упругости, с которой деформированная (натянутая) нить действует на тело.
Сила натяжения нити 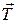 , или
, или 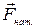 :
:
— приложена к телу,
— направлена вдоль нити от тела (рис. 48).

При решении задач мы будем считать, что нить невесомая и нерастяжимая.
Н е р а с т я ж и м а я н и т ь — это нить, изменение длины которой мы можем не учитывать: ℓнити = const.
Н е в е с о м а я н и т ь — это нить, массу которой можно не учитывать в данной задаче: 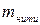 = 0.
= 0.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. От чего зависит величина силы упругости?
2. Какой силе всегда равна по модулю сила давления?
3. Что такое нерастяжимая нить?
4. Что такое невесомая нить?
| упругая деформация | elastic deformation | deformation élactique | deformación elástica |
| неупругая деформация | plastic deformation | deformation plastique | deformación plástica |
| пружина | spring | ressort | resorte |
| коэффициент | coefficient | coefficient | coeficiente |
| прямо пропорционально | directly proportional | directеment proportionel | directamente proporcional |
| растягивать | stretch | allonger | estirar |
| сила давления | force of pressure | force de pression | fuerza de presión |
| сила реакции | force of reaction | force réaction | fuerza de reacción |
| опора | support | appui | apoyo |
| сила натяжения | force of tension | force de tension | fuerza de tención |
| нить | thread | fil | hilo |
| вдоль нити | along | le long | a lo largo del hilo |
| нерастяжимый | inextensible | inextensible | no exponsible |
3.2. Силы трения
С и л ы т р е н и я — это силы, которые возникают при относительном перемещении двух твёрдых тел, находящихся в контакте друг с другом, или при наличии тенденции к перемещению.
Силы трения направлены по прямой линии, касательной к поверхности контакта.
Рассмотрим два вида трения:
— трение покоя (тело не движется относительно опоры, но имеет тенденцию к перемещению);
— трение скольжения (тело движется по поверхности опоры).
С и л а т р е н и я п о к о я 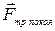 возникает тогда, когда на тело действует внешняя сила
возникает тогда, когда на тело действует внешняя сила 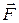 , но тело остаётся в покое.
, но тело остаётся в покое.
Для данного тела и данной опоры модуль силы трения покоя — переменная величина:
0 ≤ 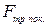 ≤
≤ 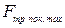
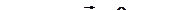 Модуль силы трения покоя всегда равен модулю силы, которая действует на тело параллельно горизонтальной поверхности контакта (рис. 49, а):
Модуль силы трения покоя всегда равен модулю силы, которая действует на тело параллельно горизонтальной поверхности контакта (рис. 49, а):
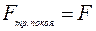 .
.
Сила трения покоя равна нулю, если на тело не действует сила, параллельная горизонтальной поверхности опоры (рис. 49,б).
Модуль силы трения покоя не может быть больше некоторого максимального значения. Модуль максимальной силы трения покоя мы можем найти по формуле 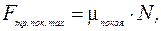
где μпокоя — коэффициент трения покоя. Коэффициент трения покоя зависит:
— от материалов поверхностей тел, которые находятся в контакте (дерево, железо, лёд и т.д.),
— от качества поверхностей тел, которые находятся в контакте (гладкая поверхность, шероховатая поверхность).
 С и л а т р е н и я с к о л ь ж е н и я возникает при движении тела по поверхности другого тела. Сила трения скольжения всегда направлена в сторону, противоположную направлению вектора относитель- ной скорости тел (рис. 50)
С и л а т р е н и я с к о л ь ж е н и я возникает при движении тела по поверхности другого тела. Сила трения скольжения всегда направлена в сторону, противоположную направлению вектора относитель- ной скорости тел (рис. 50) 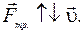
|
Модуль силы трения скольжения мы определяем по формуле
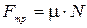 ,
,
где m — коэффициент трения скольжения. Величина этого коэффициента зависит от материала и качества поверхностей тел. Коэффициент трения скольжения определяется опытным путём.
Для данного тела и данной опоры модуль силы трения скольжения — постоянная величина.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. От чего зависит величина коэффициента трения?
2. Когда возникает сила трения покоя? Какое направ-
ление она имеет?
3. Когда возникает сила трения скольжения?
4. Какое направление имеет сила трения
скольжения?
| сила трения | force of friction | force de frottement | fuerza de fricción |
| трение скольжения | friction of sliding | frottement de glissement | fricción de declio |
| трение покоя | friction of rest | frottement de repos | fricción de reposo |
| контакт | contact | contact | contacto |
| качество | quality | qualité | cualidad |
| поверхность | surface | surface | superficia |
| шероховатая поверхность | rough surface | surface rugueuse | superficial rugosa |
3.3. Силы гравитации
Закон всемирного тяготения
|
 С и л ы г р а в и т а ц и и (силы притяжения) — это силы, с которыми все тела в природе притягиваются друг к другу.
С и л ы г р а в и т а ц и и (силы притяжения) — это силы, с которыми все тела в природе притягиваются друг к другу.
Закон всемирного тяготения для материальных точек сформулировал И. Ньютон в 1667 году.
Силы притяжения между двумя материальными точками прямо пропорциональны произведению их масс и обратно пропорциональны квадрату расстояния между ними (рис. 51):
 . (Ⅱ.3)
. (Ⅱ.3)
Коэффициент пропорциональности G называется гравитационной постоянной.
Величина и размерность G зависят от выбора системы единиц.
В СИ G = 6,67×10 - 11 Н×м2/кг2.
В системе СГС G = 6,67×10 - 8 дн×см2/г2 .
Значение гравитационной постоянной получено экспериментально.
Примером сил гравитации является сила притяжения Земли. Сила притяжения Земли — это сила, с которой Земля действует на Солнце, на Луну, на человека, на камень и т.д. Силу притяжения Земли называют с и л о й т я ж е с т и.



 С и л а т я ж е с т и (на Земле)— это сила, с которой Земля притягивает тело. Сила тяжести приложена к телу и направлена к центру Земли. Под действием силы тяжести тело движется с ускорением
С и л а т я ж е с т и (на Земле)— это сила, с которой Земля притягивает тело. Сила тяжести приложена к телу и направлена к центру Земли. Под действием силы тяжести тело движется с ускорением 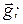
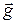 — это ускорение свободного падения (ускорение силы тяжести).
— это ускорение свободного падения (ускорение силы тяжести).
По второму закону Ньютона
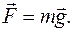 (Ⅱ.4)
(Ⅱ.4)
Из формул (Ⅱ.З) и (Ⅱ4) следует равенство:
 ,
,
где r = Rз + H, M3 — масса Земли.
Отсюда находим формулу для ускорения свободного падения (рис. 52)
 , (Ⅱ.5)
, (Ⅱ.5)
где Rз — радиус Земли, Н— высота над поверхностью
Земли. Из формулы (Ⅱ.5) видно, что:
1) ускорение свободного падения зависит от высоты над поверхностью Земли Н: чем больше Н, тем меньше ускорение свободного падения. Однако если Н << Rз (Rз = 64×105м), мы можем считать, что в этом случае ускорение свободного падения g не зависит от Н (говорят: тело находится около поверхности Земли). При Н << Rз для ускорения свободного падения мы получаем формулу: 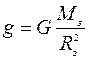 ;
;
2) ускорение свободного падения зависит от радиуса Земли. Мы знаем, что радиус Земли не постоянная величина и изменяется от максимального значения на экваторе до минимального значения
на полюсе. Поэтому в разных точках Земли ускорение свободного падения имеет разные значения;
3) ускорение свободного падения не зависит от массы тела. В данной точке Земли около ее повер- хности все тела имеют одинаковое ускорение свободного падения. При решении задач мы считаем, что g = 9,8 м/с2, что соответствует среднему значению ускорения свободного падения около Земли.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. От чего зависит ускорение свободного падения?
2. Что такое сила тяжести? Как она направлена?
3. Одинаковая ли будет величина ускорения свобод- ного падения у поверхности Луны и у поверхности Земли? Почему?
4. Чем больше масса тела, тем больше ускорение свободного падения этого тела. Это правильно?
3.4. Вес тела. Невесомость
В е с т е л а — это сила, с которой тело действует на горизонтальную опору или растягивает вертикальную нить (пружину) в уравновешенном состоянии.
Вес тела можно измерить с помощью динамометра (рис. 53).
На тело, подвешенное к динамометру, действуют две силы: сила тяжести  и сила упругости растянутой пружины
и сила упругости растянутой пружины 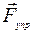 .
.
Деформацию пружины вызывает сила, действующая на пружину — вес тела 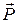 .
.
Из третьего закона Ньютона следует, что модуль веса тела равен модулю силы упругости пружины:
P = Fynp.
Вычислим вес тела в различных случаях.


а б в
1. Система «динамометр — тело» относительно Земли не движется или движется равномерно по вертикали (вверх или вниз):
 = 0 или
= 0 или  = const (рис. 53, а).
= const (рис. 53, а).
По второму закону Ньютона
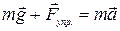
В проекциях на вертикальную ось координат 0У:
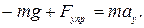
При ау = 0 Þ Fупр. = P = mg, т. е. вес численно равен силе тяжести P = mg.
2. Система «динамометр―тело» движется с уско- рением, направленным вертикально вниз (рис. 53, б).
По второму закону Ньютона
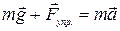 .
.
В проекциях на вертикальную ось координат 0У:
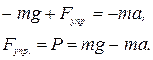
При  вес тела уменьшается P < mg, т.е. вес тела меньше силы тяжести на величину ma:
вес тела уменьшается P < mg, т.е. вес тела меньше силы тяжести на величину ma:
P = mg - та.
!!! Если система движется с ускорением 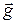 , то вес тела равен нулю: Р = 0 — система находится в состоянии н е в е с о м о с т и. В состоянии невесомости тело не деформирует (не растягивает) пружину.
, то вес тела равен нулю: Р = 0 — система находится в состоянии н е в е с о м о с т и. В состоянии невесомости тело не деформирует (не растягивает) пружину.
Состояние невесомости испытывают космонавты в кабине спутника при движении по орбите вокруг Земли.
3. Система «динамометр—тело» движется с уско- рением, направленным вертикально вверх (рис. 53, в).
По второму закону Ньютона
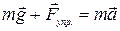 .
.
В проекциях на ось ОУ
- mg + Fynp. = ma,
Fynp. = P = mg + ma.
При  вес тела P > mg, т.е. вес больше силы тяжести на величину та:
вес тела P > mg, т.е. вес больше силы тяжести на величину та:
P = mg + ma.
| притягивать, -ся | attract | attirer | atraer |
| притяжение | attraction | attraction | atracción |
| всемирное тяготение | universal gravitation | gravitation universelle | gravitación universal |
| обратно пропорционально | inversely proportional | inversement proportionel | inversamente proporcional |
| гравитационная постоянная | gravitational constant | constant de gravitation | constantа gravitación |
| сила тяжести | force of gravity | force de pesanteur | fuerza de gravidad |
| шар | sphere | corps sphèrique | glоbo |
| полюс | pole | pôle | polo |
| экватор | equator | équateur | ecuador |
| вес | weight | poids | peso |
| невесомость | weight-lessness | impondèrabilité | imponderabilidad |
4. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА СИСТЕМЫ ТЕЛ
4.1. Система тел
|
В н у т р е н н и е с и л ы — это силы, с которыми тела данной системы действуют друг на друга.
 Рассмотрим систему, которая состоит из двух тел: тело 1 — тело 2 (рис. 54).
Рассмотрим систему, которая состоит из двух тел: тело 1 — тело 2 (рис. 54).
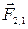 — сила, с которой тело 1 действует на тело 2;
— сила, с которой тело 1 действует на тело 2;
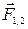 — сила, с которой тело 2 действует на тело 1;
— сила, с которой тело 2 действует на тело 1;
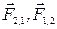 — это внутренние силы.
— это внутренние силы.
По третьему закону Ньютона эти силы:
— имеют равные модули ( 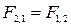 );
);
— имеют противоположные направления 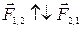 , т.е.
, т.е. 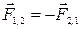 ;
;
— приложены к разным телам.

|
Тело 3 на рис. 54 не входит в систему тел «1—2», поэтому  и
и 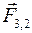 — это внешние силы.
— это внешние силы.
Система тел называется и з о л и р о в а н н о й (зáмкнутой), если на телá системы:
1) не действуют внешние силы;
2) действуют уравновешенные внешние силы, т. е. векторная сумма внешних сил равна нулю.
П р и м е р. Рассмотрим систему «Земля—тело» (рис. 55). 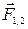 и
и 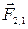 — это внутренние силы. При движении тела относительно Земли действие Солнца, Луны и планет можно не учитывать. Поэтому система «Земля—тело» — изолированная система тел.
— это внутренние силы. При движении тела относительно Земли действие Солнца, Луны и планет можно не учитывать. Поэтому система «Земля—тело» — изолированная система тел.
 П р и м е р. Рассмотрим систему тел 1—2 (рис. 56). Опора и Земля не входят в данную систему. Поэтому
П р и м е р. Рассмотрим систему тел 1—2 (рис. 56). Опора и Земля не входят в данную систему. Поэтому 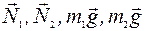 — внешние силы. Векторная сумма внешних сил, действующих на каждое тело системы, равна нулю.
— внешние силы. Векторная сумма внешних сил, действующих на каждое тело системы, равна нулю.
Значит, систему тел «1—2» мы можем считать изолированной.
4.2. Закон сохранения импульса
Рассмотрим систему из двух тел «1—2» (рис. 57):
 а) два тела массами т1 и т2 движутся
а) два тела массами т1 и т2 движутся
навстречу друг другу по горизонтальной гладкой опоре (трения нет). Скорости тел до удара  и
и 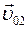 ;
;
б) тело 1 сталкивается с телом 2 (удар);
в) после удара телá движутся со скоростями
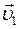 и
и 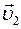 .
.
При ударе (столкновении) изменяются импульсы тел, так как изменяются скорости тел.
Изменение импульса каждого тела за время удара Δt мы можем найти по второму закону Ньютона.
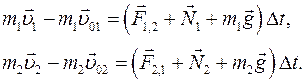
Hайдём сумму изменений импульсов тел системы «1—2». Для этого сложим полученные уравнения
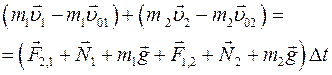 (Ⅱ.6)
(Ⅱ.6)
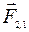 и
и 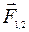 — это внутренние силы.
— это внутренние силы. 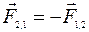 , поэтому
, поэтому 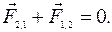
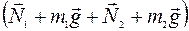 — это векторная сумма внешних сил (Земля и опора не входят в систему тел «1—2»). Так как
— это векторная сумма внешних сил (Земля и опора не входят в систему тел «1—2»). Так как 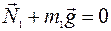 и
и 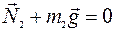 , то
, то 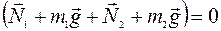 , т. е. система тел «1—2» изолированная. Тогда из формулы (II.6) получим, что
, т. е. система тел «1—2» изолированная. Тогда из формулы (II.6) получим, что
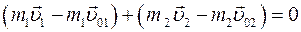 ,
,
откуда следует равенство:
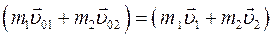 .
.

| векторная сумма импульсов тел системы до взаимодействия | векторная сумма импульсов тел системы после взаимодействия |
|
Векторная сумма импульсов тел изолирован- ной системы не изменяется при любых взаимо- действиях тел в системе:
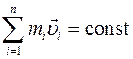 .
.
Если сумма проекций всех внешних сил на какое−либо направление равна нулю, то сумма проекций импульсов всех тел изолированной на это направление системы постоянна:
―если 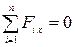 , то
, то 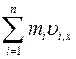 = const;
= const;
―если 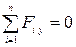 , то
, то 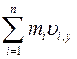 = const.
= const.
Закон сохранения импульса мы используем при изучении упругого и неупругого удара тел.
 У п р у г и й у д а р. При упругом ударе происходит упругая деформация тел; после упругого удара тела движутся отдельно, с разными скоростями, как на рис. 57.
У п р у г и й у д а р. При упругом ударе происходит упругая деформация тел; после упругого удара тела движутся отдельно, с разными скоростями, как на рис. 57.
Н е у п р у г и й у д а р. При неупругом ударе происходит неупругая деформация; после неупругого удара тела движутся вместе, с одинаковой скоростью.
Рассмотрим систему тел «1—2». Будем считать, что трения нет. Найдём скорость тел после неупругого удара (рис. 58).
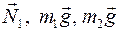 — внешние силы, так как опора и Земля не входят в систему тел «1—2». Скорость тел после удара мы можем найти по закону сохранения импульса системы тел, если система тел «1—2» изолированная. Сумма проекций внешних сил на ось ОХ равна нулю:
— внешние силы, так как опора и Земля не входят в систему тел «1—2». Скорость тел после удара мы можем найти по закону сохранения импульса системы тел, если система тел «1—2» изолированная. Сумма проекций внешних сил на ось ОХ равна нулю:  , поэтому система «1—2» изолированная в направлении ОХ. Напишем закон сохранения импульса в проекциях на ось ОХ:
, поэтому система «1—2» изолированная в направлении ОХ. Напишем закон сохранения импульса в проекциях на ось ОХ:
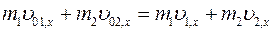
При неупругом ударе 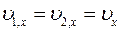 , следовательно,
, следовательно,
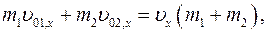
откуда находим скорость тел после удара
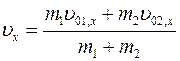 .
.
???ОТВЕТЬТЕ НА ВОПРОСЫ:
1. После какого удара тела имеют одинаковые скорости?
2. При каком условии импульс системы тел — постоянная величина?
3. Что такое внешняя сила?
4. Что такое внутренние силы?
5. В каком случае сила нормальной реакции опоры — внешняя сила?
6. В каком случае мы можем считать систему тел изолированной в направлении ОХ?
| сохранение | conservation | conservation | conservación |
| система | system | système | sistema |
| внешняя сила | external force | force extérieure | fuerza exterior |
| внутренняя сила | internal force | force intérieure | fuerza interior |
| изолированная (замкнутая) система | isolated (closet) system | système fermé (isolé) | sistema cerrado |
| удар | collision | collision | colisión |
5. ДИНАМИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ПО ОКРУЖНОСТИ
 Из второго закона Ньютона следует, что направление ускорения тела всегда совпадает с направлением результирующей силы, действующей на тело
Из второго закона Ньютона следует, что направление ускорения тела всегда совпадает с направлением результирующей силы, действующей на тело  . Направление скорости тела
. Направление скорости тела 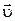 может совпадать и не совпадать с направлением силы.
может совпадать и не совпадать с направлением силы.
Если скорость тела направлена вдоль линии действия силы, то движение прямолинейное (рис. 59).
Если вектор скорости составляет с вектором силы угол a: 0 < a < 180°, то движение криволинейное (рис. 60).
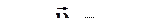 В частном случае криволинейного движения — равномерного движения по окружности (см. с. 40)
В частном случае криволинейного движения — равномерного движения по окружности (см. с. 40)
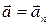 , поэтому
, поэтому 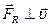 : результирующая сила изменяет направление скорости, но не изменяет величину скорости.
: результирующая сила изменяет направление скорости, но не изменяет величину скорости.
П р и м е р. Рассмотрим движение спутника Земли. Спутник Земли — это тело, которое движется по замкнутой траектории вокруг Земли. Траектория спутника называется орбитой. Найдём приближённую формулу скорости спутника, который движется по окружности на высоте Н над поверхностью Земли (рис. 61).
 Предположим, что спутнипк движется равномерно по окружности со скоростью
Предположим, что спутнипк движется равномерно по окружности со скоростью 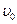 . Радиус окружности (орбиты) R = RЗ + H. Во время движения на спутник действует только сила притяжения Земли
. Радиус окружности (орбиты) R = RЗ + H. Во время движения на спутник действует только сила притяжения Земли 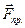 Действие других сил можно не учитывать:
Действие других сил можно не учитывать:
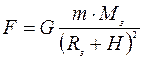
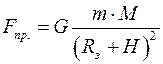 ,
,
где т — масса спутника, Мз — масса Земли, Rз― радиус Земли).
При равномерном движении по окружности ускорение тела направлено по радиусу к центру окружности и равно
 .
.
Второй закон Ньютона для спутника в скалярном виде в проекциях на мгновенную ось, направленную по радиусу к центру запишется в виде
 или
или 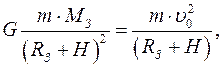
откуда следует формула скорости спутника:

Если спутник движется около поверхности Земли, т. е. ( 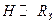 ), то
), то 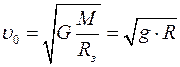 .
.
Из последней формулы следует, что скорость спутника вблизи поверхности Земли — величина постоянная, она выражается через ускорение свободного падения и радиус Земли. Эта скорость называется первой космической скоростью, её величина 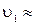 8 км/с.
8 км/с.
Первый искусственный спутник Земли был запущен советскими учёными и инженерами в
1957 году.
| Основные формулы динамики | |
Второй закон Ньютона:
 Третий закон Ньютона
Третий закон Ньютона
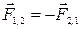 Закон сохранения импульса
(для изолированной системы тел)
Закон сохранения импульса
(для изолированной системы тел)
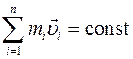
| В и д ы с и л
Сила упругости (закон Гука)
Fупр.х= - k×x
Сила трения скольжения
Fтр. = m×N
Сила гравитации
Закон всемирного тяготения:
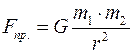 Сила тяжести
Сила тяжести
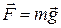 Ускорение свободного падения
у поверхности Земли
Ускорение свободного падения
у поверхности Земли
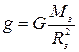
|
Скорость спутника на высоте Н над Землёй
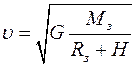
|
III. МЕХАНИЧЕСКАЯ РАБОТА И ЭНЕРГИЯ
1. МЕХАНИЧЕСКАЯ РАБОТА
Механическую работу совершает сила, если точка приложения силы перемещается.
1.1. Работа постоянной силы
Определим понятие механической работы для случая:
— на тело действует постоянная сила 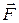 = const,
= const,
— угол между направлениями вектора силы и вектора перемещения не изменяется a = const (рис. 62).

М е х а н и ч е с к а я р а б о т а постоянной силы — это физическая величина, равная произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между их направлениями:
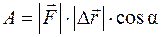 (III.1)
(III.1)
Так как  (см. рис. 62), то можно записать:
(см. рис. 62), то можно записать:
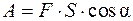 .
.
Работа — скалярная величина.
В формуле (III.1) 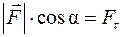 — проекция вектора силы на направление перемещения
— проекция вектора силы на направление перемещения 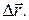
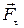 — тангенциальная составляющая силы
— тангенциальная составляющая силы 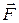 . Поэтому формулу работы (III.1) можно записать так:
. Поэтому формулу работы (III.1) можно записать так:
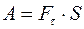 . (Ⅲ.2)
. (Ⅲ.2)
При 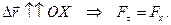 Тогда
Тогда 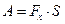 .
.
Работу совершает только тангенциальная составляющая силы 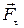 . Нормальная составляющая силы
. Нормальная составляющая силы 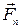 перпендикулярна направлению перемещения;
перпендикулярна направлению перемещения; 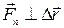 и она работу не совершает (см. рис. 62).
и она работу не совершает (см. рис. 62).
Из формулы (III. 1) следует:
— сила совершает положительную работу, если  [0, 90°[, т. е. cos a > 0; А > 0.
[0, 90°[, т. е. cos a > 0; А > 0.
— сила совершает отрицательную работу, если  ] 90°, 180°], т. е. cos a < 0; А < 0.
] 90°, 180°], т. е. cos a < 0; А < 0.
Если на тело действуют несколько сил, то каждая сила совершает работу.
Полная работа сил, действующих на тело, равна алгебраической сумме работ, которые совершаются этими силами.

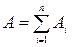 . (III.3)
. (III.3)
Рассмотрим пример (рис. 63). На тело, которое движется прямолинейно и равномерно по горизонтальной плоскости, действуют четыре силы:
 и сила
и сила 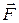 .
.
(  , поэтому F = Fтр. и N = mg).
, поэтому F = Fтр. и N = mg).
Работа силы тяжести равна нулю, так как 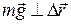 .
.
Работа силы реакции опоры равна нулю, так как  .
.
Работу совершают только две силы:
—сила 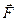 АF = F×Δr×cos0°ÞАF = F×S
АF = F×Δr×cos0°ÞАF = F×S
—сила трения АFтр=Fтр×Δr×cos1800 Þ
Þ Атрения = - Fтр.×S.
Полную работу сил находим по формуле (III.3):
Аполная = Атяги + Атрения
Аполная = F×S +( - Fтр.×S),
но F = Fтр. , поэтому Аполная = 0
Этот результат можно получить из формулы
(III. 1). Равнодействующая всех сил, действующих на тело при прямолинейном равномерном движении, равна нулю 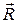 = 0:
= 0:
АR = R×Δr×cosa = 0.
Сделаем вывод. Работа равнодействующей силы равна алгебраической сумме работ составляющих сил.
Единицы работы:
[A] = [F] × [Δr].
Единица работы в СИ — 1 джоуль:
[A] = 1 Дж = 1 Н×м Þ 1 Дж = 1 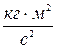 .
.
Единица работы в системе СГС — 1 эрг:
[А] = 1 эрг = 1 дин×см Þ 1 эрг = 1 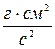 .
.
Соотношение между единицами работы:
1 Дж = 1 Н×м = 105дин×102см = 107эрг.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. При каких условиях сила совершает механическую работу?
2. В каком случае сила совершает: а) положительную работу? б) отрицательную работу?
3. Совершает ли работу сила тяжести при переме- щении тела: а) по горизонтали? б) по наклонной плоскости?
4. Совершается ли работа при прямолинейном равномерном движении?
1.2. Работа переменной силы
Работу переменной силы можно вычислить следующим образом:
— разделим весь путь на n малых перемещений 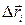 , так, что на каждом малом перемещении приближённо выполняется условие
, так, что на каждом малом перемещении приближённо выполняется условие 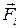 = const и
= const и 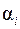 = const;
= const;
― вычислим элементарную работу 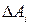 по формуле (III.1) на каждом малом перемещении
по формуле (III.1) на каждом малом перемещении 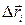 :
:
 ΔAi = Fi× Δri × cosai ;
ΔAi = Fi× Δri × cosai ;
― вычислим работу на всём пути по формуле (III.3)
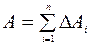
при n ® ¥ 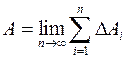 . (III.4)
. (III.4)
Механическую работу постоянной силы и переменной силы можно вычислить графически.
На графике F = F (х), где F = const, работа постоянной силы определяется величиной площади прямоугольника BEDC (рис. 64, а)
A = F ×½(x2 –x1)½ = DC × BC = SBEDC.
 На графике F = F (х), где F ¹ const, работа переменной силы определяется величиной площади фигуры KLMN (рис. 64, б).
На графике F = F (х), где F ¹ const, работа переменной силы определяется величиной площади фигуры KLMN (рис. 64, б).
П р и м е р. Вычислим графически работу переменной силы, которая растягивает пружину (рис. 65):
F = k×x,
где х — координата конца пружины.
График зависимости F = F (x) ― прямая линия, которая проходит через начало координат.
Пусть величина силы изменяется от F1 = k×x1 до F2 = k×x2.
|