КИНЕМАТИКА РАВНОМЕРНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ
 Д в и ж е н и е т о ч к и п о о к р у ж н о с- т и — это криволинейное периодическое движение.
Д в и ж е н и е т о ч к и п о о к р у ж н о с- т и — это криволинейное периодическое движение.
Т р а е к т о р и я д в и ж е н и я — кривая линия — окружность (рис. 38). На рисунке 38:
точка А — положение материальной точки в момент времени t0;
точка В — положение материальной точки в момент времени t;
А︶В — дуга, которую проходит материальная точка за интервал времени Δt = t - t0;
S — путь, который проходит точка, равен длине дуги А︶В;
точка 0 — центр окружности и начало координат;
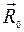 и
и 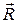 — радиусы-векторы материальной точки в моменты времени t0 и t;
— радиусы-векторы материальной точки в моменты времени t0 и t;
Δφ — угол поворота радиуса-вектора, за интервал времени Δt.
Длина окружности ℓ = 2πR, где R — радиус окружности.
|
П е р и о д в р а щ е н и я — это время одного оборота. Период обозначается буквой Т.
Единица измерения периода в СИ и в системе СГС — одна секунда [T] = 1 с.
Ч а с т о т а в р а щ е ни я — это физическая величина, равная числу оборотов, которые совершает точка за единицу времени. Если за интервал времени Δt точка сделала n оборотов, то частота равна
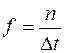 , при этом Dt = n× T, тогда
, при этом Dt = n× T, тогда 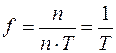
Связь между периодом Т и частотой f:
 .
.
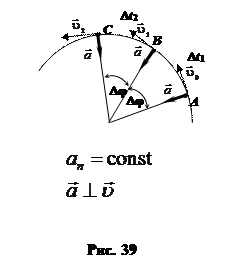 Единица частоты в СИ и в системе СГС — один оборот в секунду: [ f] = 1/с = 1 с -1.
Единица частоты в СИ и в системе СГС — один оборот в секунду: [ f] = 1/с = 1 с -1.
Как мы уже знаем (стр.24) мгновенная л и н е й н а я с к о р о с т ь — это физическая величина, равная пределу отношения перемещения к интервалу времени, за который это перемещение совершается, когда Δt® 0 (Δt стремится к нулю):
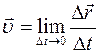 .
.
При равномерном движении по окружности (рис. 39):
— материальная точка проходит дуги равной длины за равные интервалы времени: длина дуги А︶В = S1, длина дуги В︶С = S2. При Δt1 = Δt2
А︶В = В︶С, то есть S1 = S2;
— модуль линейной скорости не изменяется
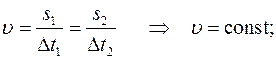
— за время, равное одному периоду, тело проходит путь, равный длине окружности, то есть,
если Δt = T, то S = 2πR,
поэтому модуль линейной скорости равен  .
.
Вектор линейной скорости в каждый момент времени направлен по касательной к окружности.
Так как v = const, то тангенциальное ускорение равно нулю 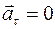 .
.
Так как направление вектора линейной скорости изменяется, то нормальное ускорение не равно нулю:  Можно доказать, что модуль нормального ускорения определяется по формуле
Можно доказать, что модуль нормального ускорения определяется по формуле 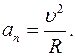
Полное ускорение 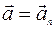 .
.
В каждой точке окружности вектор ускорения направлен по радиусу к центру окружности 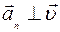 .
.
Ускорение точки при равномерном движении по окружности (нормальное ускорение) называют центростремительным ускорением.
У г л о в а я с к о р о с т ь — это физическая величина, равная пределу отношения угла поворота радиуса-вектора точки к интервалу времени, за который этот поворот происходит, когда Δt® 0 (Δtстремится к нулю):
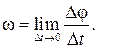
Единица угловой скорости в СИ и системе СГС — 1 радиан в секунду [ω] = 1 рад/с =1 с-1.
(Угол в 1 радиан — это центральный угол, дуга которого по длине равна радиусу окружности: 2π радиан =360°, поэтому 1 радиан » 57,3°.)
При равномерном движении по окружности:
— радиус-вектор точки за равные интервалы времени делает повороты на равные углы
Δφ1 = Δφ2 = ¼ при Δt1 = Δt2 =¼;
— модуль угловой скорости — постоянная величина:
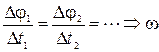 = const;
= const;
— за время, равное одному периоду,
угол поворота радиуса-вектора равен Δφ = 2π радиан
то есть, если Δt = Т, то Δφ = 3600 = 2π ,
поэтому формула угловой скорости 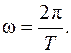
Из сравнения формул угловой и линейной скорости между ними следует связь:

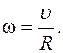
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Почему равномерное движение по окружности — это периодическое движение?
2. Какой путь проходит точка за время, равное одному периоду?
3. Как направлен вектор центростремительного ускорения?
| окружность | circumference | circonférence | circunferencia |
| вращение | rotation | rotation | rotación |
| дуга | arc | arc | arco |
| периодическое движение | periodic motion | mouvement périodique | movimiento periódico |
| период | period | périod | período |
| оборот | revolution | tour | revolución |
| частота | frequency | fréquence | frequencia |
| линейная скорость | linear velocity | vitesse linéaire | velocidad lineal |
| радиус | radius | rayon | radio |
| поворот | rotation | rotation | vuelta |
| угловая скорость | angular velocity | vitesse angulaire | velocidad angular |
| Основные формулы кинематики Формулы прямолинейного равномерного движения в проекциях на ось координат ОХ: | |||
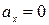
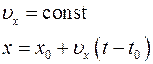
| 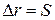 если
если 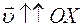 , то , то 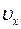 > 0
если > 0
если 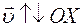 , то , то 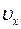 < 0 < 0
| ||
| Формулы прямолинейного равнопеременного движения (равноускоренного движения, равнозамедленного движения) в проекциях на ось координат ОХ | |||
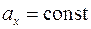
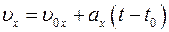
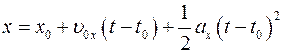


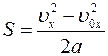
| 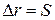
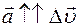 ! всегда !
При равноускоренном
движении
v> v0, поэтому ! всегда !
При равноускоренном
движении
v> v0, поэтому 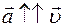 При равнозамедленном
движении
v< v0, поэтому
При равнозамедленном
движении
v< v0, поэтому  v0 х ― проекция скорости
v0 х ― проекция скорости 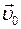 на ось 0Х
v0― модуль скорости на ось 0Х
v0― модуль скорости 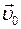 vх ― проекция скорости
vх ― проекция скорости  на ось ОХ
v― модуль скорости на ось ОХ
v― модуль скорости  ах ― проекция вектора ускорения на ось ОХ
а ― модуль вектора ускорения
ах ― проекция вектора ускорения на ось ОХ
а ― модуль вектора ускорения
|
| Формулы равномерного движения по окружности | |
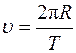 = 2πRf = 2πRf

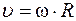 , , 
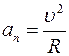
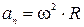
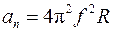
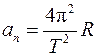
|
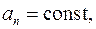 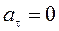
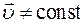 , , 
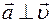

|
Ⅱ. ДИНАМИКА
Динамика — это часть механики, которая изучает механическое движение тел и причины, вызывающие изменение характеристик этого движения.
Дата добавления: 2015-09-28; просмотров: 1365;

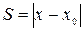
 , если v> v0
, если v> v0  , если v< v0
, если v< v0