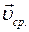Умножение вектора на скаляр
Пусть заданы вектор  и скаляр n. Найдём произведение вектора
и скаляр n. Найдём произведение вектора  и скаляра n.
и скаляра n.
В результате умножения вектора на
скаляр мы получаем новый вектор  :
:
 = n ·
= n ·  (рис. 11).
(рис. 11).
Направление вектора  такое же, как направление вектора
такое же, как направление вектора  при n > 0.
при n > 0.
Направление вектора  противоположно направлению вектора
противоположно направлению вектора  при n < 0.
при n < 0.
Модуль вектора  в n раз больше модуля вектора
в n раз больше модуля вектора  , если n >1.
, если n >1.
3.5. Разложение вектора на составляющие
Разложить вектор  на составляющие векторы по двум зáданным направлениям — это значит найти два вектора
на составляющие векторы по двум зáданным направлениям — это значит найти два вектора  и
и  :
:
— направления которых совпадают c зáданными направлениями;
— сумма которых равна вектору  .
.

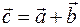
Геометрически разложить вектор на составляющие векторы — это значит построить параллелограмм по зáданной диагонали и зáданным направлениям сторон.
Найдём составляющие вектора  по зáданным направлениям АВ и CD. (рис. 12):
по зáданным направлениям АВ и CD. (рис. 12):
1. Через начало и конец вектора  проводим прямые линии, параллельные одному из зáданных направлений (АВ).
проводим прямые линии, параллельные одному из зáданных направлений (АВ).
2. Через начало и конец вектора  проводим прямые линии, параллельные второ- му зáданному направлению (CD).
проводим прямые линии, параллельные второ- му зáданному направлению (CD).
Мы построили парал- лелограмм.
|
3. Зáданный вектор  направлен по диагонали параллелограмма, построенного на искомых составляющих векторах
направлен по диагонали параллелограмма, построенного на искомых составляющих векторах  и
и  :
: 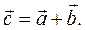 Начала векторов
Начала векторов  ,
,  ,
,  находятся в одной точке.
находятся в одной точке.
3.6. Проекция вектора на оси координат
 П р о е к ц и я в е к т о р а н а о с ь — это скалярная величина, равная произведению модуля вектора на косинус угла между направлением вектора и положительным направлением оси (рис. 13, а):
П р о е к ц и я в е к т о р а н а о с ь — это скалярная величина, равная произведению модуля вектора на косинус угла между направлением вектора и положительным направлением оси (рис. 13, а):
 — это вектор;
— это вектор;
cх — это проекция вектора  на ось ОХ;
на ось ОХ;
c у — это проекция вектора  на ось ОУ;
на ось ОУ;
a — это угол между вектором  и осью ОХ;
и осью ОХ;
b — это угол между вектором  и осью OУ
и осью OУ
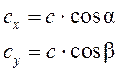
Так как
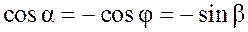 и
и
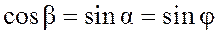
(рис.13, а), то
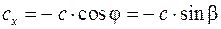 и
и 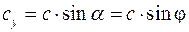
На рис.13, б:
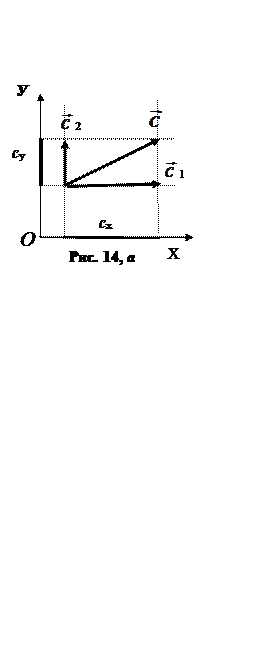 cх — это графическое изображение проекции вектора
cх — это графическое изображение проекции вектора  на ось OX;
на ось OX;
c у — это графическое изображение проекции вектора  на ось OУ
на ось OУ
Найдём проекции вектора  на оси координат 0Х и 0У в прямоугольной (декартовой) системе координат (рис. 14, а, б, в, г) методом разложения вектора на составляющие:
на оси координат 0Х и 0У в прямоугольной (декартовой) системе координат (рис. 14, а, б, в, г) методом разложения вектора на составляющие:
1. Разложим вектор  на два составляющих вектора
на два составляющих вектора 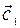 и
и 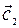 ;
;
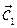 — составляющий вектор по оси ОХ;
— составляющий вектор по оси ОХ;
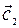 — составляющий вектор по оси ОУ.
— составляющий вектор по оси ОУ.
2. Проекция вектора  на ось ОХ равна модулю составляющего вектора
на ось ОХ равна модулю составляющего вектора  со знаком «плюс» или «минус»:
со знаком «плюс» или «минус»:
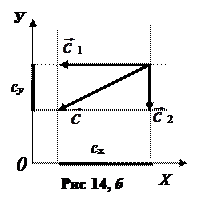 cх >0, если
cх >0, если  (рис. 14, а; рис. 14, г);
(рис. 14, а; рис. 14, г);
cх < 0, если 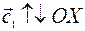 (рис. 14, б; рис. 14, в).
(рис. 14, б; рис. 14, в).
3. Проекция вектора 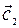 на ось ОУ равна модулю составляющего вектора
на ось ОУ равна модулю составляющего вектора 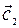 со знаком «плюс» или «минус»:
со знаком «плюс» или «минус»:
cу >0, если 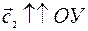 (рис. 14, а; рис. 14, в)
(рис. 14, а; рис. 14, в)
су < 0, если 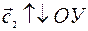 (рис. 14, б; рис. 14, г)
(рис. 14, б; рис. 14, г)
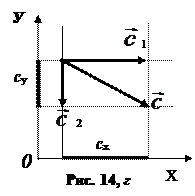 | |||
 | |||
Рассмотрим частные случаи

а б а б
Рис. 15 Рис. 16
Так как вектор  и
и 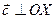 (рис. 15, а), то cу = +с и cх = 0
(рис. 15, а), то cу = +с и cх = 0
Так как вектор 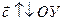 и
и 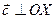 (рис. 15, б), то cу = - с и cх = 0
(рис. 15, б), то cу = - с и cх = 0
Так как вектор 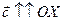 и
и 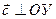 (рис. 16, а), то cх = +с и cу = 0
(рис. 16, а), то cх = +с и cу = 0
Так как вектор 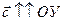 и
и 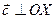 (рис. 16, б), то cх = - с и cу = 0
(рис. 16, б), то cх = - с и cу = 0
Можно решить обратную задачу: если мы знаем проекции вектора, то
мы можем найти сам вектор, т. е. найти модуль вектора и направление
вектора (рис. 17).
Модуль вектора 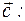
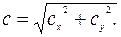
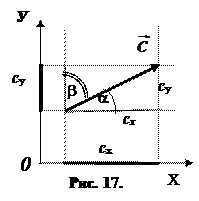 |
Направление вектора  определяют углы a и b:
определяют углы a и b:

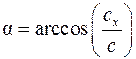
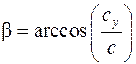
Или из рис. 17 следует:
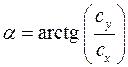 .
.
Зачем нам нужно знать проекции вектора? Так как проекции векторов на оси координат — это скалярные величины, мы можем заменить любое векторное равенство (уравнение) системой скалярных равенств (уравнений). При этом геометрические действия с векторами мы заменяем алгебраическими действиями с проекциями векторов.
!!! 3апомните правила:
Проекция результирующего вектора (вектора суммы) на данную ось равна алгебраической сумме проекций составляющих (слагаемых) векторов на эту же ось:
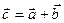 ; ; 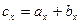 ; ; 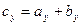
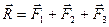 ; ; 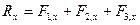 ; ; 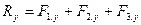 Проекция вектора разности на данную ось равна разности проекций уменьшаемого и вычитаемого векторов на эту же ось.
Проекция вектора разности на данную ось равна разности проекций уменьшаемого и вычитаемого векторов на эту же ось.
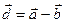 ; ; 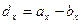 ; ; 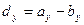
|
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Какие векторные величины вы знаете?
2. Какие скалярные величины вы знаете?
3. В каком случае модуль результирующего вектора равен:
а) сумме модулей составляющих векторов?
б) разности модулей составляющих векторов?
4. Можно ли сказать, что 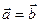 , если:
, если:
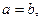
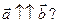
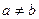 ,
, 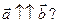
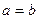 ,
, 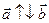 ?
?
5. В каком случае проекция вектора на ось координат:
а) положительная величина? б) отрицательная величина?
в) равна нулю? г) равна модулю вектора со знаком «+»?
д) равна модулю вектора со знаком « - »?
| параллельные линии | parallel lines | lignes parallèles | lineas paralelas |
| противоположные векторы | opposite vectors | vecteurs de sens opposés | vectores anti-paralelos |
| геометрический | geometric | géométrique | geométrico |
| параллелограмм | parallelogram | parallèlogramm | paralelogramo |
| треугольник | triangle | triangle | triangulo |
| составляющий вектор | component vector | vecteur composant | vector componente |
| результирующий вектор | resulting vector | vecteur résultant | vector resultante |
| совпадать | coincide | coincider | coincidir |
| сторона | side | coté | lado |
| ось | axis | axe | eje |
| диагональ | diagonal | diagonal | diagonal |
| разложение | decomposition | décomposition | decomposicion |
| проекция | projection | projection | proyeccion |
| система координат | system of coordinates | système de coordonnées | sistema de coordinadas |
| перпендикуляр | perpendicular | perpendiculaire | perpendicular |
| прямоугольный | rectangular | rectangulaire | rectángulo |
МЕХАНИКА

Механика изучает механическое движение.
М е х а н и ч е с к о е д в и ж е н и е — это процесс изменения положения тела относительно другого тела, которое мы условно считаем неподвижным и называем телом отсчёта.
Ⅰ. КИНЕМАТИКА
К и н е м a т и к а — это часть механики, которая изучает механическое движение, но не учитывает причины, вызывающие это движение.
Задача кинематики ¾ ввести физические величины, которые характеризуют механическое движение и установить соотношения между ними.
1. ОСНОВНЫЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ КИНЕМАТИКИ
Мы изучаем движение материальной точки.
1.1. Материальная точка
М а т е р и а л ь н а я т о ч к а — это физическое тело, форму и размеры которого мы можем не учитывать в данной задаче.
Например: Земля движется вокруг Солнца. Размеры Солнца и Земли меньше, чем расстояние между Солнцем и Землёй. В этом случае мы можем считать, что Солнце и Земля — материальные точки.
1.2 . Траектория
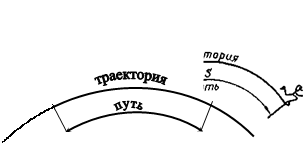
Т р а е к т о р и я — это линия, которую описывает материальная точка при движении (рис. 18).
 | |||
 | |||
а б
Рис. 18
Эта траектория (рис. 18, а) — кривая линия. Движение материальной точки к р и в о л и н е й н о е.
Эта траектория (рис. 18, б) — прямая линия. Движение материальной точки п р я м о л и н е й н о е.
1.3. Путь
П у т ь — это скалярная, всегда положительная физическая величина, которая равна длине траектории. Путь обозначается буквой S (читаем «эс»).
Путь измеряется в единицах длины.
Единица пути в СИ: [S] = 1 м.
Единица пути в системе СГС: [S] = 1 см.
Внесистемная единица пути: [S] = 1 км.
1.4. Время
Время — скалярная физическая величина. Момент времени обозначается символом t.
Интервал времени — это разность между двумя моментами времени.
Интервал времени обозначается символом Δt (читаем «дельта тэ»):
Δt = t– t0,
где t — это любой момент времени,
t0 — это начальный момент времени.
Единица времени в СИ и в системе СГС [t] = l с.
| механика | mechanics | mécanique | mecánica |
| кинематика | kinematics | cinématique | cinemática |
| изменение | change | variation | cambio |
| положение | position | position | posición |
| относительно | relatively | relativementà | en relación |
| покой | rest | repos | reposo |
| материальная точка | material point | point matériel | point material |
| траектория | trajectory | trajectoire | trayectoria |
| путь | path | distance | camino |
| внесистемная единица | non-system unit | unité hors système | unidad fuera del sistema |
| момент времени | moment of time | moment du temps | momento de tiempo |
| интервал времени | interval of time | intervalle du temps | intervalo de tiempo |
1.5. Тело отсчёта
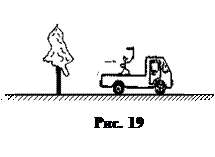 Т е л о о т с ч ё т а — это тело, относительно которого мы рассматриваем движение данного тела.
Т е л о о т с ч ё т а — это тело, относительно которого мы рассматриваем движение данного тела.
По дороге движется автомобиль, в котором находится человек (рис. 19).
В о п р о с: движется или не движется человек?
О т в е т:
— человек движется относительно дерева (дерево — это тело отсчёта);
— человек не движется (находится в покое) относительно автомобиля (автомобиль — это другое тело отсчёта).
Мы видим, что человек движется относительно одного тела отсчёта (дерева) и не движется относительно другого тела отсчёта (автомобиля).
С д е л а е м в ы в о д: движение и покой — относительные состояния.
1.6. Система координат
Мы определяем положение материальной точки её координатами в выбранной нами с и с т е м е к о о р д и н а т (рис. 20). Точка О — это начало координат.
Положение точки на прямой линии определяет одна координата (см. рис. 20, а).
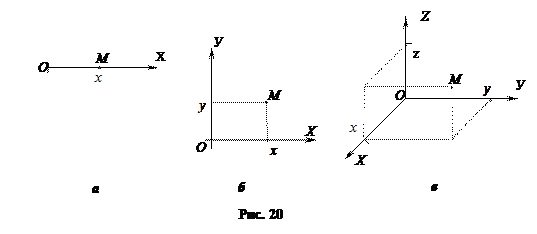 |
Положение точки на плоскости определяют две координаты (см. рис. 20, б).
Положение точки в пространстве определяют три координаты (см. рис. 20, в).
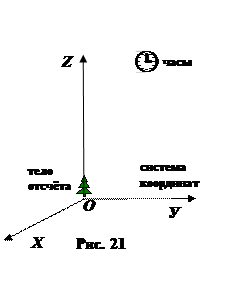 1.7. Система отсчёта
1.7. Система отсчёта
Мы изучаем движение тела в системе отсчёта (рис. 21).
Система отсчёта — это тело отсчёта + система координат, связанная с телом отсчёта + секундомер.
Тело отсчёта нужно, чтобы определить, движется данное тело или находится в покое в данной системе отсчёта.
Система координат нужна для определения положения тела относительно тела отсчёта.
Секундомер (часы) — это прибор для измерения времени.
| тело отсчёта | body of reference | Corps de référence | cuerpo de referencia |
| система отсчёта | system of reference | système de référence | sistema de referencia |
1.8. Радиус-вектор 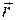
Нарисуем точку М в системе координат XOУ (рис. 22).
Р а д и у с − в е к т о р точки — это вектор,
который соединяет начало координат с данной точкой.
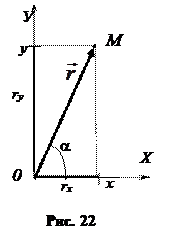
Если мы знаем радиус-вектор (его модуль r и направление, которое задано углом a), то мы можем найти координаты точки М:
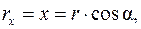
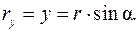
Если мы знаем координаты точки М (х, у), то мы можем найти радиус-вектор:
— модуль радиуса-вектора
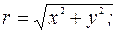
— его направление, которое определяет угол a: 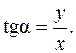
— Радиус-вектор 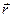 и координаты точки х, у — это характеристики положения материальной точки.
и координаты точки х, у — это характеристики положения материальной точки.
1.9. Перемещение 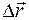
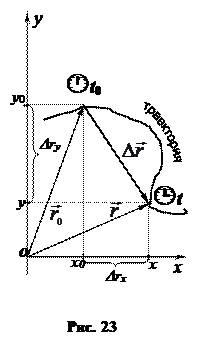 При движении материальной точки ее радиус- вектор и координаты изменяются (рис. 23). За интервал времени Δt радиус-вектор изменяется на величину
При движении материальной точки ее радиус- вектор и координаты изменяются (рис. 23). За интервал времени Δt радиус-вектор изменяется на величину
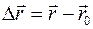 .
.
Вектор 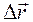 — это перемещение материальной точки (тела) за интервал времени Δt = t – t0.
— это перемещение материальной точки (тела) за интервал времени Δt = t – t0.
П е р е м е щ е н и е 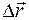 — это вектор, который соединяет начальное и конечное положения материальной точки на траектории.
— это вектор, который соединяет начальное и конечное положения материальной точки на траектории.
Если материальная точка движется криволинейно, то путь S и модуль перемещения Δr не равны (  ; S > Δr; рис. 24, а).
; S > Δr; рис. 24, а).
Если материальная точка движется прямолинейно, то путь S и модуль перемещения Δr равны (S = Δr; рис. 24, б).
Перемещение, так же как и путь, измеряется в единицах длины [Δr] = [S] = [ℓ].
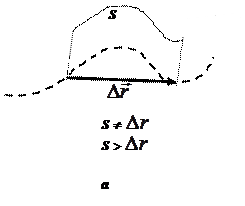 | |||||||
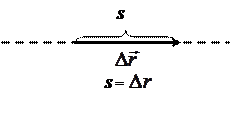 | |||||||
| |||||||
|
| радиус-вектор | radius-vector | rayon-vecteur | radio-vector |
| перемещение | displacement | déplacement | desplacimienta |
1.10. Скорость 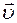

|
Автомобиль движется быстрее человека: скорость автомобиля больше скорости человека.
С р е д н я я с к о р о с т ь — это векторная физическая величина, равная отношению вектора перемещения к интервалу времени, за который это перемещение происходит:
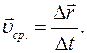
Единица скорости в СИ: [υ] = 1 м/с (один метр в секунду).
Единица скорости в системе СГС: [υ] = 1 см/с.
Внесистемная единица скорости: [υ] = 1 км/ч; 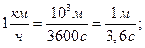
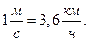
На практике мы часто используем понятие средней скорости по пути.
С р е д н я я с к о р о с т ь п о п у т и — это скалярная физическая величина, равная отношению пути к интервалу времени, за который тело проходит этот путь:
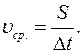
.
 М г н о в е н н а я с к о р о с т ь — это скорость, которую имеет тело в данный момент времени (в данной точке траектории).
М г н о в е н н а я с к о р о с т ь — это скорость, которую имеет тело в данный момент времени (в данной точке траектории).
Чтобы найти мгновенную скорость, надо рас- сматривать перемещение за бесконечно малый интер- вал времени (интервал времени стремится к нулю):
Δt ® 0
М г н о в е н н а я с к о р о с т ь — это векторная
физическая величина, равная пределу отношения вектора перемещения к интервалу времени Δt, за который это перемещение происходит, когда Δt ® 0:
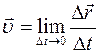 .
.
Символ lim в формуле обозначает слово «предел».
Вектор мгновенной скорости направлен по прямой линии, касательной к траектории в данной точке (рис. 25).
| быстрота | rapidity | rapidité | rapidez |
| средняя скорость | mean velocity | vitesse moyenne | velocidad media |
| мгновенная скорость | instant velocity | vitesse instantanée | velocidad instantánea |
| стремиться к нулю | tend to zero | tendre vers zéro | tender a cero |
| предел | limit | limite | límite |
| касательный | tangent | tangente | tangente |

1.11. Изменение скорости 
Скорость тела не изменяется: 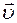 = const, если:
= const, если:
— модуль скорости не изменяется: 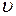 = const;
= const;
— направление скорости не изменяется.
Скорость тела изменяется 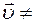 const, если:
const, если:
— модуль скорости изменяется, или
— направление скорости изменяется, или
— модуль и направление скорости изменяются.
Вектор изменения скорости 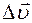 равен разности векторов скорости
равен разности векторов скорости 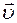 и
и 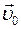 (рис. 26):
(рис. 26):
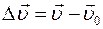 ,
,
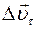 (читаем «дельта вэ тау») — это вектор, характеризующий изменение вектора скорости по модулю:
(читаем «дельта вэ тау») — это вектор, характеризующий изменение вектора скорости по модулю:

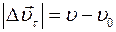
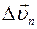 (читаем «дельта вэ эн») — это вектор, характеризующий изменение вектора скорости по направлению.
(читаем «дельта вэ эн») — это вектор, характеризующий изменение вектора скорости по направлению.
|
 ½АВ½ = ½АD½ =
½АВ½ = ½АD½ = 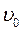 , ½АС½ =
, ½АС½ = 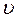 , ½DС½ =
, ½DС½ = 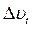 , ½ВD ½=
, ½ВD ½= 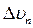
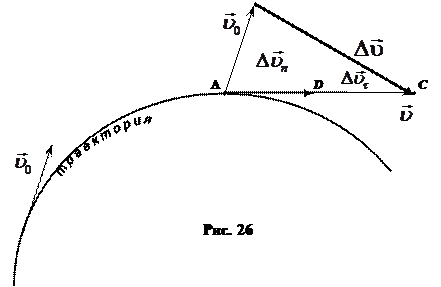 |
Полное изменение вектора скорости равно:
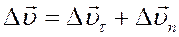 .
.
1.12. Ускорение 
Ускорение характеризует быстроту изменения скорости.
С р е д н е е у с к о р е н и е — это векторная физическая величина, равная отношению изменения скорости к интервалу времени, за который это изменение происходит:
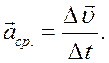
Вектор среднего ускорения направлен так же, как вектор изменения скорости 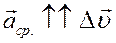
Мгновенное ускорение 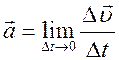
 Единица ускорения в СИ: [а] = 1 м/с2 (один метр в секунду в квадрате).
Единица ускорения в СИ: [а] = 1 м/с2 (один метр в секунду в квадрате).
Единица ускорения в системе СГС: [а] = 1 см/с2.
Вектор ускорения имеет два перпендикулярных составляющих: нормальное ускорение 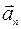 и тангенциальное ускорение
и тангенциальное ускорение 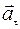 (рис. 27).
(рис. 27).
Н о р м а л ь н о е у с к о р е н и е характеризует изменение вектора скорости по направлению
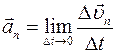 .
.
Вектор нормального ускорения всегда направлен перпендикулярно вектору скорости: 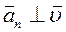 ,
, 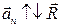 .
.
Если направление вектора скорости не изменяется, то нормальное ускорение равно нулю.
Т а н г е н ц и а л ь н о е у с к о р е н и е характеризует изменение вектора скорости по модулю
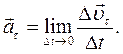

Вектор тангенциального ускорения и вектор скорости могут иметь одинаковые или противоположные направления:
— если модуль скорости увеличивается, то вектор тангенциального ускорения и вектор скорости имеют одинаковые направления: 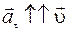 − это ускόренное движение (рис. 27);
− это ускόренное движение (рис. 27);
— если модуль скорости уменьшается, то вектор тангенциального ускорения и вектор скорости имеют противоположные направления 
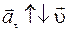 − это замéд- ленное движение.
− это замéд- ленное движение.
Если модуль скорости не изменяется, то тангенциальное ускорение равно нулю.
П о л н о е у с к о р е н и е — это сумма нормального ускорения и тангенциального ускорения:
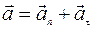 .
.
Модуль полного ускорения
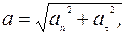 так как
так как 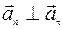 .
.
| ускорение | acceleration | accélération | acceleración |
| тангенциальный | tangent | tangentiele | tangencial |
| нормальный | normal | normale | normal |
| полный | total | totale | total |
Дата добавления: 2015-09-28; просмотров: 1061;