ПРЕДМЕТ ФИЗИКА
1.1. Что изучает физика?
Физика — это наука о природе. Физика изучает физические тела, физические процессы и физические явления.
Например:
— стол, дом, Солнце, вода, воздух — это физические тела;
— камень падает — это физический процесс;
— автобус движется — это физический процесс;
— идёт дождь — это физическое явление.
| физика | physics | physique | fisica |
| изучать | study | étudier | estudiar |
| природа | nature | nature | naturaleza |
| тело | body | corps | cuerpo |
| процесс | process | processus | proceso |
| явление | phenomenon | phenomène | phenómeno |
1.2. Физическая величина
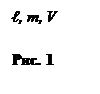
 Ф и з и ч е с к а я в е л и ч и н а — это характеристика физического тела, физического процесса, физического явления.
Ф и з и ч е с к а я в е л и ч и н а — это характеристика физического тела, физического процесса, физического явления.
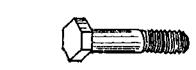
Пример (рис. 1). Это тело. Тело имеет массу, длину, объем. Длина, масса, объем — это характеристики тела.
Длина, масса, объем — это физические величины.
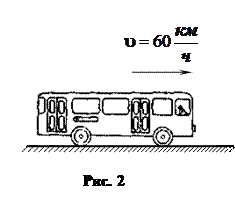 Пример (рис. 2). Это автобус. Автобус движется.
Пример (рис. 2). Это автобус. Автобус движется.
Скорость автобуса равна 60 км/ч (шестидесяти километрам в час).
Скорость — это характеристика движения (характеристика физического процесса).
Скорость — это физическая величина.
Физические величины мы обозначаем буквами латинского алфавита и греческого алфавита, например:
— массу мы обозначаем буквой m (читаем «эм»),
— длину мы обозначаем буквой ℓ (читаем «эль»),
— время мы обозначаем буквой t (читаем «тэ»),
— плотность мы обозначаем буквой ρ (читаем «ро»).
| физическая величина | physical quantity | grandeur physique | magnitude física |
| характеристика | characteristic | caractéristique | caracteristica |
| движение | motion | mouvement | movimiento |
| длина | length | longueur | longitud |
| масса | mass | masse | masa |
| время | time | temps | tiempo |
| обозначать | designate | désigner | señalar |
1.3. Методы определения физических величин
 Как мы можем найти физическую величину? Физическую величину мы можем измерить.
Как мы можем найти физическую величину? Физическую величину мы можем измерить.
Пример (рис. 3).
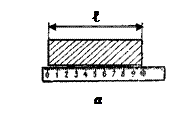
1. Длину тела ℓ мы измеряем линейкой (рис. 3, а). Линейка — это прибор для измерения длины.
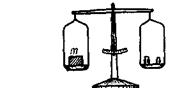
2. Массу тела m мы измеряем на весах (рис. 3, б). Весы — это прибор для измерения массы.
3.  Время t мы измеряем секундомером (рис. 3, в). Секундомер (часы) — это прибор для измерения времени.
Время t мы измеряем секундомером (рис. 3, в). Секундомер (часы) — это прибор для измерения времени.
|
 Физическую величину мы можем найти по формуле.
Физическую величину мы можем найти по формуле.
Пример (рис. 4). Тело имеет форму параллелепипеда. Объем параллелепипеда мы определяем по формуле.
|
|
 Длину ℓ, ширину b, толщину d мы измеряем линейкой.
Длину ℓ, ширину b, толщину d мы измеряем линейкой.
Если мы знаем массу тела m и объем V, то мы можем найти плотность вещества ρ (читаем «ро») по формуле
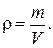
Мы можем найти по формулам и другие физические величины, например скорость, силу, работу.
С д е л а е м в ы в о д ы:
1) физическую величину мы можем измерить физическим прибором;
2) физическую величину мы можем найти по формуле.
| метод | method | méthode | methodó |
| найти | find | trouver | encontrar |
| измерить | measure | mesurer | medir |
| прибор | device | appareil | aparato |
| шкала | scale | échelle | escala |
| линейка | roule | règle | regla |
| весы | balance | balance | pesa |
| секундомер | stop-watch | chronomètre | chronómetro |
| формула | formula | formula | formula |
| объём | volume | volume | volumen |
| плотность | density | densité | densidad |
| вещество | matter | matière | substancia |
| сделать вывод | make a conclusion | faire une conclusion | sacar conclusiones |
| толщина | thickness | épaisseur | gordura |
| ширина | width | largeur | anchura |
| высота | height | hauteur | altura |
| сила | force | force | fuerza |
| скорость | velocity | vitesse | velocidad |
| работа | work | travail | trabajo |
1.4. Единицы измерения физических величин
Е д и н и ц ы д л и н ы
|
1 км = 1000 м (один километр равен тысяче метров),
1 м = 100 см (один метр равен ста сантиметрам),
1см = 10 мм (один сантиметр равен десяти миллиметрам).
Единица измерения обозначается символом физической величины в квадратных скобках:
[ℓ] = 1 м, [ℓ] = 1 см, [ℓ] = 1 км.
Е д и н и ц ы м а с с ы
1 кг (один килограмм), 1 г (один грамм),
1 т (одна тонна) — это единицы массы.
[m] = 1 кг, [m] = 1 г, [m] == 1 т.
1 т = 1000 кг (в одной тонне — тысяча килограммов),
1 кг = 1000 г (в одном килограмме — тысяча граммов),
1 г =1000 мг (в одном грамме — тысяча миллиграммов).
Е д и н и ц ы в р е м е н и
1 ч (один час), 1 мин (одна минута), 1 с (одна секунда) — это единицы времени.
[t] = 1 ч, [t] = 1 мин., [t] = 1 с.
1 ч = 60 мин (один час равен шестидесяти минутам),
1 мин. = 60 с (одна минута равна шестидесяти секундам),
1 ч = 3600 с (один час равен трём тысячам шестистам секундам).
|
Рассмотрим некоторые производные единицы измерения.
Е д и н и ц ы о б ъ ё м а
Формула объема параллелепипеда V = ℓ·b·d. В этой формуле ℓ, b и d измеряются в единицах длины, например в метрах или в сантиметрах. Тогда единицы объема:
[V] = [ℓ] 3.
[V] = l м3 (один кубический метр) или [V] =1 см3 (один кубический сантиметр).
Е д и н и ц ы п л о т н о с т и
Формула плотности вещества 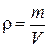 .
.
Если масса измеряется в килограммах, а объём — в кубических метрах, то единица плотности
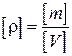 1кг/м3 (один килограмм на кубический метр).
1кг/м3 (один килограмм на кубический метр).
Единицы измерения объема, плотности, скорости, силы, работы и других физических величин — это производные единицы.
| единица измерения | unit of measurement | unité de mesure | unidad medida |
| основная единица | basic unit | unité de base | unidad básica |
| производная единица | derived unit | unité dérivée | unidad derivada |
| символ | symbol | symbole | símbolo |
| подставить | substitute | mettre | meter |
1.5. Система единиц
Система единиц состоит из основных и производных единиц.
|
единица длины [ℓ] = 1 м — один метр,
единица массы [m] = 1 кг — один килограмм,
единица времени [t] = 1 с — одна секунда.
Единицы измерения других физических
величин — производные единицы:
единица скорости [υ] = 1 м/с — один метр в секунду,
единица ускорения [а] = 1 м/с2 — один метр на секунду в квадрате,
единица силы [F] — 1 кг·м/с2 = 1 Н — один ньютон,
единица работы [А] = 1 Н·м = 1 Дж — один джоуль,
единица плотности [ρ] = 1 кг/м3 — один килограмм на кубический метр.
| Основные механические единицы в СГС: |
|
единица массы [m] = 1 г (один грамм),
единица времени [t] = 1 с (одна секунда).
Некоторые производные единицы в СГС:
единица скорости [υ] = 1 см/с,
единица ускорения [а] = 1 см/с2,
единица силы [F] = 1 г×см/с2 = 1 дин — одна дина,
единица работы [А] = 1 дин·см = 1 г×см 2 /с2 = 1 эрг.
Мы можем переводить единицы измерения из одной системы единиц в другую. Например, единица плотности в СИ [ρ] = 1 кг/м3. Найдем значение этой единицы в системе СГС:
1 кг/м3 = 1 кг/1м3 = 103 г/106 см3= 10-3 г/см3.
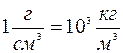
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Что изучает физика?
2. акие физические тела вы знаете?
3. Какие физические величины вы знаете?
4. Каким прибором мы измеряем длину?
5. Какую физическую величину измеряют секундомером?
6. Сколько сантиметров в одном километре?
7. Сколько секунд в одном часе?
| система единиц | system of units | système dˊunités | sistema de unidad |
| Международная система (СИ) | International System | Système International | Systema Internacional |
| значение | value | valeur | valor |
| переводить единицы | transform units | convertir des unités | transformar unidades |
| система СГС | system CGS | système CGS | systema CGS |
2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
2.1. Скалярные величины
С к а л я р н а я в е л и ч и н а — это физическая величина, которая имеет численное значение и единицу измерения.
Скалярная величина может быть положительной или отрицательной.
Примеры скалярных величин: температура, масса, объём, время, плотность. Математические действия со скалярными величинами — это алгебраические действия с числами.
 2.2. Векторные величины
2.2. Векторные величины
В е к т о р н а я в е л и ч и н а — это физическая величина, которая имеет:
1) численное значение, которое всегда положительно (модуль вектора);
2) направление;
3) единицу измерения.
Примеры векторных физических величин: скорость, ускорение, сила.
Векторная величина обозначается буквой и стрелкой над этой буквой. Например:
— вектор скорости обозначается символом 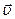 ,
,
— вектор ускорения обозначается символом  ,
,
 — вектор силы обозначается символом
— вектор силы обозначается символом 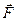 .
.
Модуль вектора обозначается так:
½ 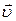 ½ или υ — модуль вектора
½ или υ — модуль вектора 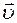 ,
,
½  ½ или а — модуль вектора
½ или а — модуль вектора  ,
,
| 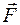 | или
| или 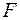 — модуль вектора
— модуль вектора 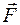 .
.
На рисунке (графически) вектор изображается направленным отрезком прямой линии (рис. 5). Модуль вектора равен длине отрезка в зáданном масштабе (рис. 6).
| скаляр | scalar quantity | grandeur scalaire | magnitude escalar |
| вектор | vector | vecteur | vector |
| численное значение | numerical value | valeur numerique | numeric valor |
| модуль | modul | module | modulo |
| направление | direction | direction | direccion |
| отрезок | segment | segment | segmento |
| стрелка | arrow, point | aiguille | aguja |
| масштаб | scale | échelle | escala |
| прямая линия | straight line | ligne droite | recta linea |
| |

3. ДЕЙСТВИЯ С ВЕКТОРАМИ
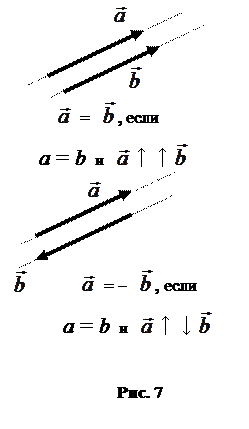 Математические действия с векторными величинами — это действия векторной алгебры.
Математические действия с векторными величинами — это действия векторной алгебры.
3.1. Сравнение векторов
Рассмотрим два вектора  и
и  (рис. 7).
(рис. 7).
Равные векторы. (  =
=  ). Два вектора равны, если они имеют:
). Два вектора равны, если они имеют:
— равные модули,
— одинаковые направления.
Равнопротивоположные векторы. (  = -
= -  ). Два вектора равнопротивоположны, если они имеют:
). Два вектора равнопротивоположны, если они имеют:
— равные модули,
— противоположные направления.
3.2. Сложение векторов
Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника.
Пусть заданы два вектора  и
и  (рис. 8).
(рис. 8).
Найдём сумму этих векторов
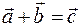 .
.
Векторы  и
и  — это составляющие векторы, вектор
— это составляющие векторы, вектор  — это результирующий вектор.
— это результирующий вектор.
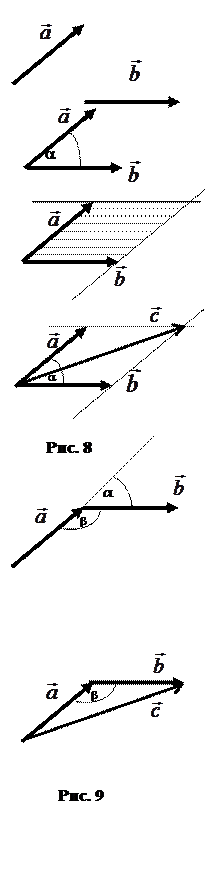
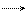
 Правило параллелограмма для сложения двух векторов:
Правило параллелограмма для сложения двух векторов:
1. Нарисуем вектор  .
.
2. Нарисуем вектор  так, чтобы его начало совпадало с началом вектора
так, чтобы его начало совпадало с началом вектора  ; угол между векторами равен a (альфа).
; угол между векторами равен a (альфа).
3. Через конец вектора  проведём
проведём
прямую линию, параллельную вектору  .
.
4. Через конец вектора  проведём
проведём
прямую линию, параллельную вектору  . Мы построили параллелограмм. Стороны этого параллелограмма — составляющие векторы
. Мы построили параллелограмм. Стороны этого параллелограмма — составляющие векторы  и
и  .
.
5. Проведем диагональ параллелограмма из общей точки начала вектора  и начала вектора
и начала вектора  .
.
6. Модуль результирующего вектора 
равен длине диагонали параллелограмма
и определяется по формуле
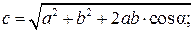
начало вектора  совпадает с началом вектора
совпадает с началом вектора  и началом вектора
и началом вектора  (направление вектора
(направление вектора  показано на рисунке).
показано на рисунке).
Правило треугольника для сложения
двух векторов (рис. 9):
1. Нарисуем составляющие векторы 
и  так, что начало вектора
так, что начало вектора  совпадает
совпадает
с концом вектора  . При этом угол между сторонами треугольника равен b (бета).
. При этом угол между сторонами треугольника равен b (бета).
2. Результирующий вектор  — это вектор, начало которого совпадает с началом вектора
— это вектор, начало которого совпадает с началом вектора  , а конец совпадает с концом вектора
, а конец совпадает с концом вектора  .
.
Модуль результирующего вектора находим по формуле
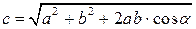 =
= 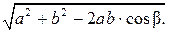
Дата добавления: 2015-09-28; просмотров: 795;
