Вычитание векторов

Пусть заданы два вектора и ;угол между векторами равен a (альфа) (рис. 10, а). Найти вектор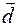

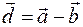. В этом выражении

вектор 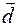—вектор разности;

вектор — уменьшаемый вектор;

вектор — вычитаемый вектор.

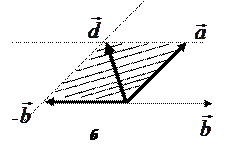Модуль вектора разности определяется по формуле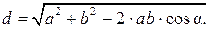

Найти разность вектора и вектора — это то же самое, что найти сумму вектора и вектора (- ) противоположного вектору :

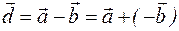
Мы можем найти (изобразить) вектор раз­ности геометрически по правилу паралле­лограмма или по правилу треугольника (рис. 10).

Правило параллелограмма. Стороны параллелограмма — вектор и век­тор (- ); диагональ параллелограмма — вектор разности 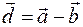(рис. 10, б).

Правило треугольника.

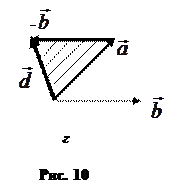Вариант 1. Если начало уменьшаемого вектора (вектора ) и начало вычитаемого вектора (вектор ) находятся в одной точке (совпадают), то вектор разности 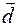направлен из конца вычитаемого вектора в конец уменьшаемого вектора (рис. 10, в)

Вариант 2. Вектор разности 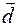соединяет начало вектора и конец вектopa (- ) (начало вектора (- ) совпадает с концом вектора ) (рис. 10, г).