Векторное произведение векторов и его свойства
Три некомпланарных вектора 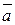 ,
, 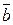 и
и 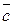 , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 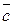 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 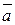 ко второму вектору
ко второму вектору 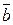 виден совершающимся против часовой стрелки, и левую, если по часовой.
виден совершающимся против часовой стрелки, и левую, если по часовой.
 правая тройка,
правая тройка, 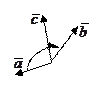 левая тройка
левая тройка
Определение. Векторным произведением вектора 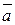 на вектор
на вектор 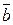 называется вектор
называется вектор 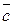 , который:
, который:
1) перпендикулярен векторам 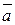 и
и 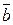 , т.е.
, т.е. 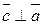 и
и 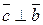 ;
;
2) имеет длину, численно равную площади параллелограмма, построенного на векторах 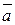 и
и 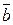 как на сторонах, т.е.
как на сторонах, т.е.
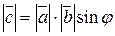 , где
, где 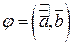 ;
;
3) векторы 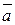 ,
, 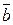 и
и 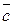 образуют правую тройку.
образуют правую тройку.
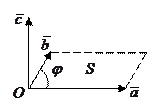
Векторное произведение обозначается 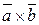 или
или 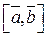 .
.
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами 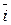 ,
, 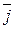 и
и 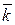 :
:
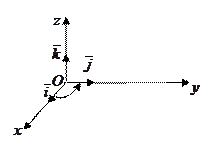
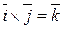 ,
, 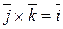 ,
, 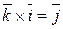 .
.
Дата добавления: 2015-10-13; просмотров: 777;
