Векторное произведение векторов
Определение 1. Векторным произведением геометрических векторов 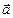 и
и 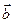 называется вектор
называется вектор 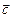 , такой что: а)
, такой что: а) 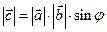 ; б)
; б) 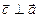 ,
, 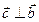 ; в) векторы
; в) векторы 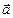 ,
, 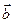 ,
, 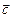 образуют правую тройку векторов.
образуют правую тройку векторов.
Для векторного произведения могут быть использованы следующие обозначения: 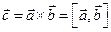 .
.
Справедливы следующие свойства векторного произведения:
1) 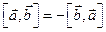 ; 2)
; 2) 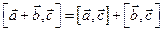 ;
;
3) 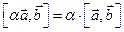 ; 4)
; 4) 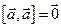 .
.
Свойства 1), 3) и 4) прямо следуют из определения векторного произведения. Свойство 2) мы принимаем без доказательства.
Еще раз подчеркнем, что результатом векторного произведения векторов является вектор, по длине равный площади параллелограмма, построенного на векторах 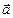 и
и 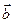 . Поэтому с помощью векторного произведения можно находить площади параллелограммов и треугольников. Кроме того, векторное произведение равно нулю тогда и только тогда, когда векторы параллельны одной прямой, что позволяет проверять коллинеарность заданных векторов.
. Поэтому с помощью векторного произведения можно находить площади параллелограммов и треугольников. Кроме того, векторное произведение равно нулю тогда и только тогда, когда векторы параллельны одной прямой, что позволяет проверять коллинеарность заданных векторов.
3. Вычислениевекторного произведения в ДСК
Теорема 2. В декартовой системе координат векторное произведение геометрических пространственных векторов 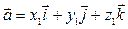 и
и 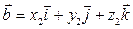 равно вектору
равно вектору 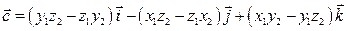 .
.
Доказательство. Рассмотрим векторное произведение векторов 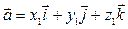 и
и 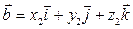 , заданных в декартовой системе координат
, заданных в декартовой системе координат 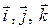 . Используя свойства 2), 3) векторного произведения векторов, запишем следующие преобразования:
. Используя свойства 2), 3) векторного произведения векторов, запишем следующие преобразования:
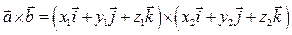
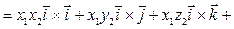
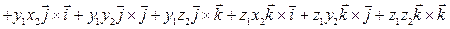 .
.
Для получения заключительного результата заметим, что в силу свойства 4 векторные произведения равных векторов равны нулевому вектору, т. е. 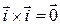 ,
, 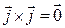 ,
, 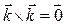 . Кроме того, из правой ориентации базисных векторов
. Кроме того, из правой ориентации базисных векторов 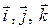 следует, что
следует, что 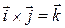 ,
, 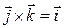 ,
, 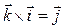 ,
, 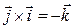 ,
, 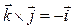 ,
, 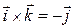 . Продолжая вычисления, получим, что
. Продолжая вычисления, получим, что 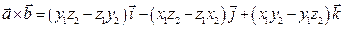 . Теорема доказана.
. Теорема доказана.
Полученный результат можно записать в виде 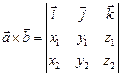 . Здесь определитель мы понимаем, как формальное разложение по своей первой строке. Иными словами, данную формулу можно описать следующим образом. В декартовой системе координат векторное произведение геометрических пространственных векторов
. Здесь определитель мы понимаем, как формальное разложение по своей первой строке. Иными словами, данную формулу можно описать следующим образом. В декартовой системе координат векторное произведение геометрических пространственных векторов 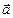 и
и 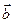 равно вектору, порождаемому определителем, у которого первая строка состоит из базисных векторов
равно вектору, порождаемому определителем, у которого первая строка состоит из базисных векторов 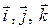 ; вторая строка состоит из координат вектора
; вторая строка состоит из координат вектора 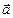 ; третья строка состоит из координат вектора
; третья строка состоит из координат вектора 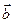 .
.
Дата добавления: 2015-10-09; просмотров: 1134;
