Векторное произведение

1)Определение ориентации тройки векторов

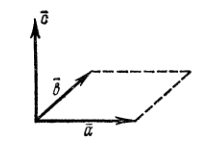
Опр.Упорядоченная тройка некомпланарных векторов называется право ориентированной или правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки.

2)Определение векторного определения

Опр.Векторным произведением вектора 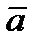на вектор 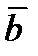называется вектор 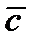, который определяется следующим образом:

1)длина вектора 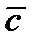равна .

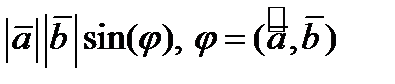2)Вектор 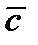перпендикулярен векторам 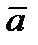и .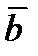

3)Векторы 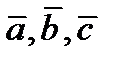образуют правую тройку.

Обозначается .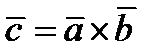

3)Задача, приводящая к векторному произведению. Вычисление скорости точки твердого тела, вращающегося вокруг неподвижной оси.

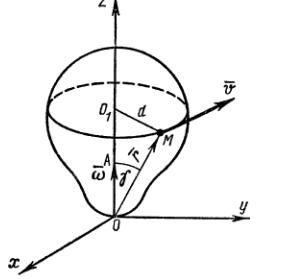
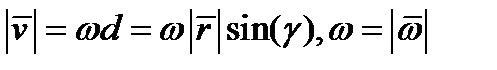
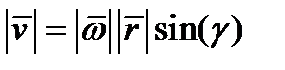
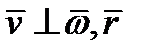и векторы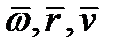

Образуют правую тройку.

.

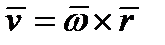4)Свойства векторного произведения.

1) 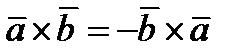. Действительно модули векторов одинаковы, а направление 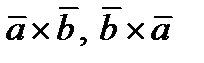противоположное.

2) 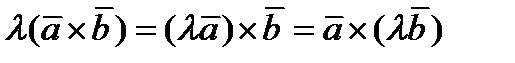. Доказательство.

Докажем, что 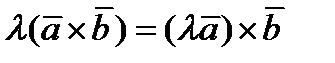. Рассмотри 2 случая 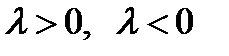, если 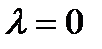, то очевидно.

а) . .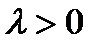

.

.

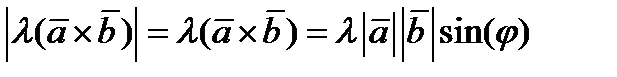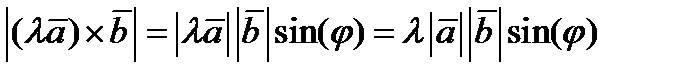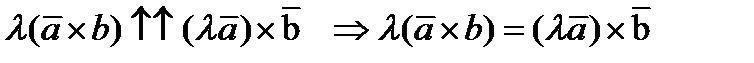б) Для случая 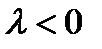и 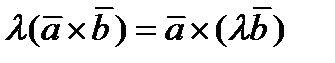докажите сами.

3) 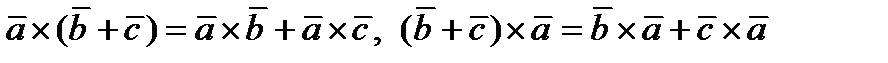. Без доказательства.

4)Для того, чтобы 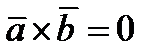необходимо и достаточно, чтобы векторы 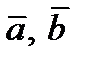были коллинеарные.

Доказательство.

Необходимость.

Дано 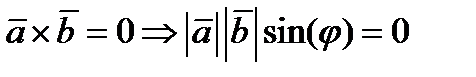. Тогда среди этих векторов есть нулевой вектор 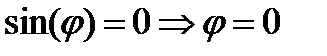или или 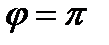. Если есть нулевой вектор, то векторы коллинеарны.

Достаточность.

Пусть векторы 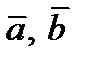коллинеарные. Тогда среди этих векторов есть или нулевой вектор 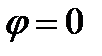или или 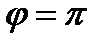. Поэтому .

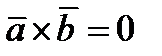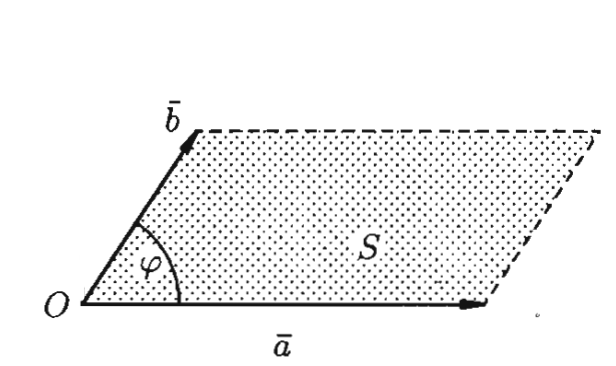
5)Геометрический смысл модуля векторного произведения .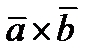

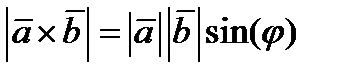– это площадь параллелограмма, построенного на векторах .

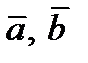Пример. Найти площадь параллелограмма, построенного на векторах . .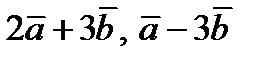

.

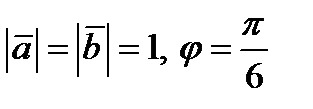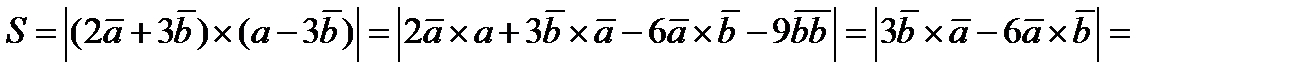
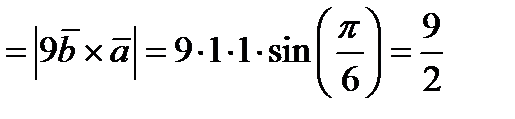5)Выражение векторного произведения через координаты перемножаемых векторов.

Пусть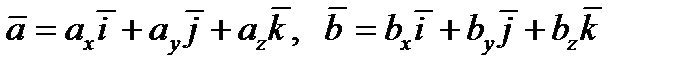

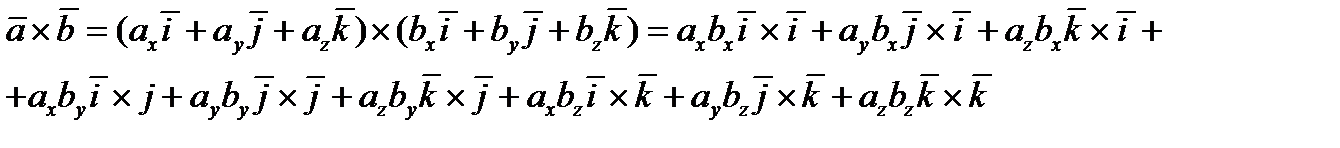
Таблица векторного произведения векторов .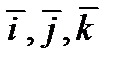

Если направление кратчайшего поворота от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору.

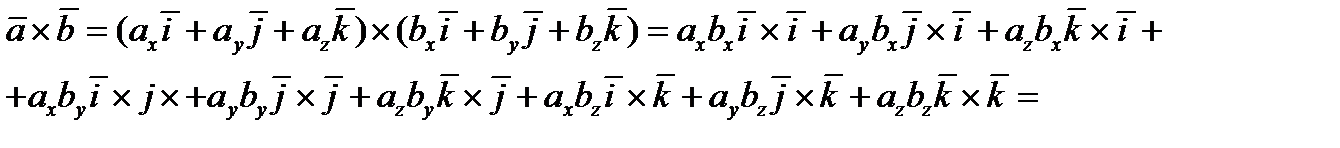
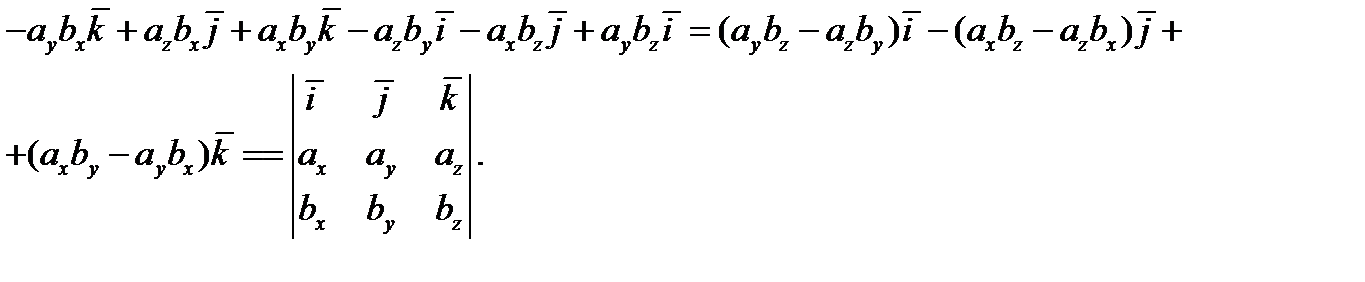
Пример. Даны точки 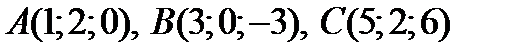.Вычислить площадь треугольника .

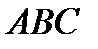Площадь треугольника 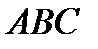равна площади треугольника, построенного на векторах 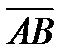и .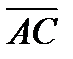

.

.

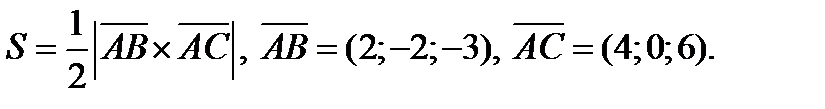
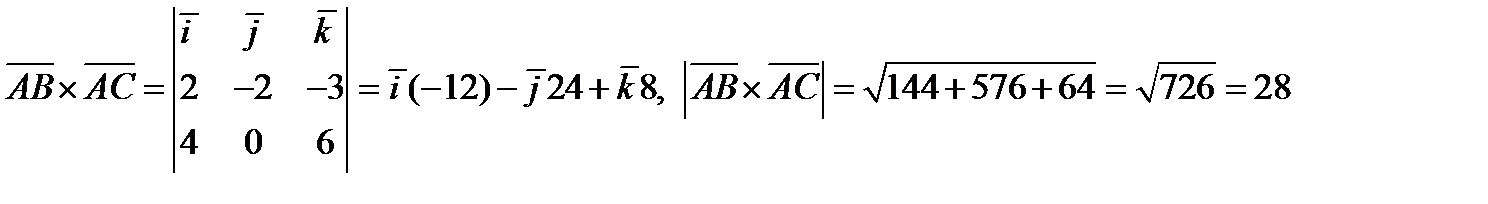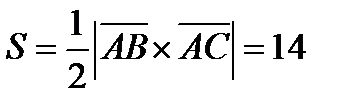§ 5 Смешанное произведение векторов

1)Определение. Способ вычисления.

Опр. Смешанным произведением трех векторов 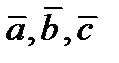называется число равное .

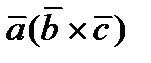Способ вычисления. Пусть .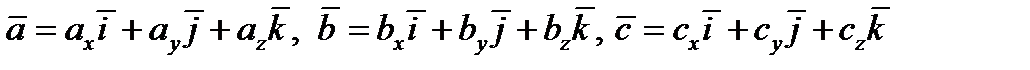

.

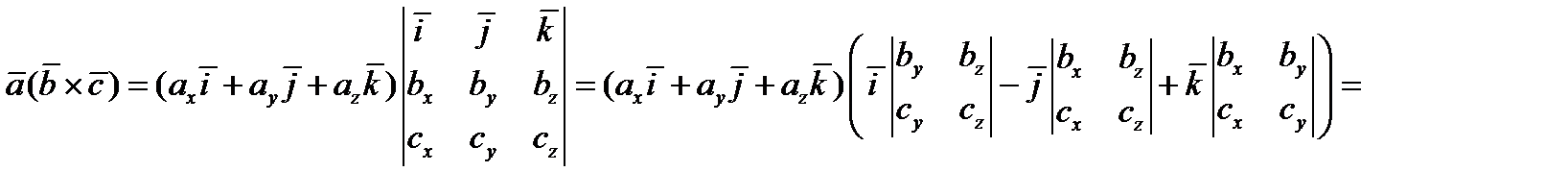
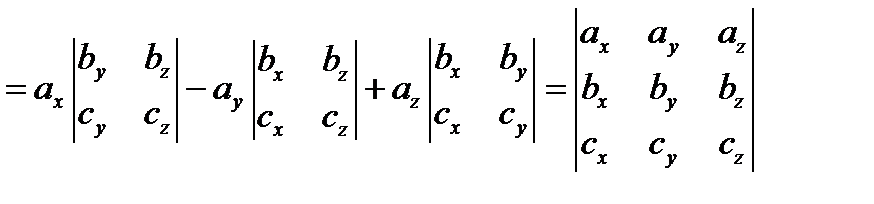2)Свойства смешанного произведения.

1) .

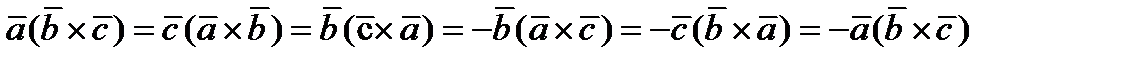Докажем, что .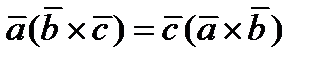

.

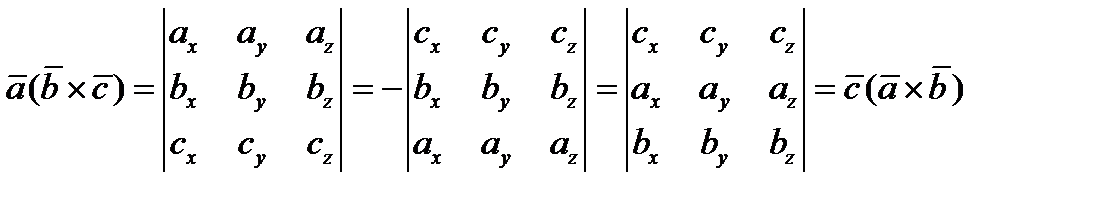Остальные равенства доказываются также. Смешанное произведение обозначается 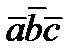, так как неважно где ставить .

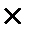2)Геометрический смысл смешанного произведения.

Модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах.

Доказательство.

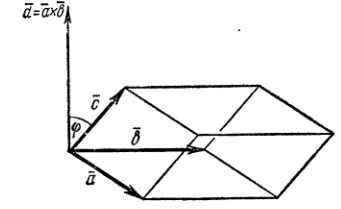Объем параллелепипеда равен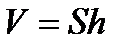

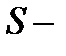площадь основания, 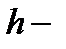параллелепипеда. . .

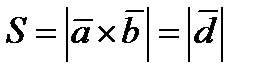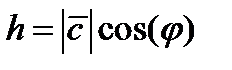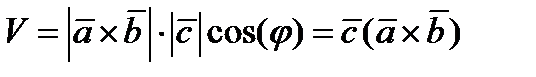
В данном доказательстве векторы 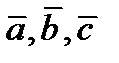образуют правую тройку. Если эти векторы образуют левую тройку, то смешанное произведение будет отрицательным. Поэтому объем .

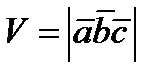Теор. Для того, чтобы три вектора были компланарны необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

Докажите сами.

Пример. Проверить, компланарны ли векторы. .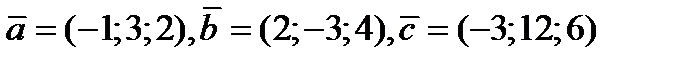

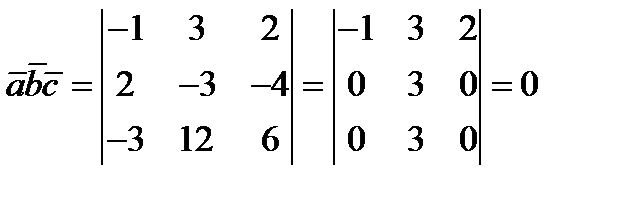
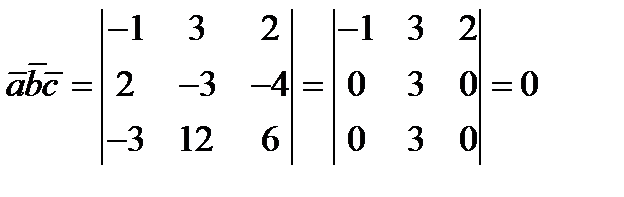.Следовательно, векторы компланарны.