Равномерное движение
При равномерном движении (рис. 28, в):
— за любые равные интервалы времени тело проходит равные отрезки пути,
— модуль скорости не изменяется,
— тангенциальное ускорение равно нулю.
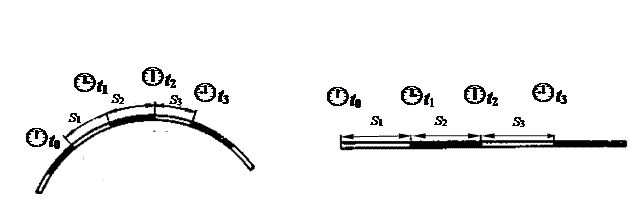
при Δt1 = Δt2 = Δt3 = … ; S1 = S2 = S3 =… и v1 = v2 = v3 =…
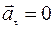
Рис. 28, в
2.4. Неравномерное движение
При неравномерном движении (рис. 28, г):
— за равные интервалы времени тело проходит неравные отрезки пути,
— модуль скорости изменяется,
— тангенциальное ускорение не равно нулю.
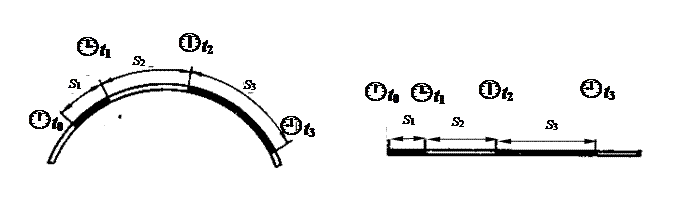
при Δt1 = Δt2 = Δt3 = … S1 ≠ S2 ≠ S3 ≠… и v1 ≠ v2 ≠ v3 ≠…
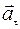 ≠ 0
≠ 0
Рис. 28, г
Неравномерное движение может быть ускóренным или замéдленным.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Что такое материальная точка? Автомобиль — это материальная точка?
2. Что характеризует мгновенная скорость?
3. Что характеризует средняя скорость?
4. Какое направление имеет мгновенная скорость?
5. При каком движении путь и модуль перемещения
равны?
6. Что характеризует нормальное ускорение?
7. Что характеризует тангенциальное ускорение?
| прямолинейный | rectilinear | rectiligne | rectilíneo |
| криволинейный | curvilinear | curviligne | curvilíneo |
| равномерный | uniform | uniforme | uniforme |
| неравномерный | non- uniform | nonuniforme | no uniforme |
| переменный | variable | variable | variable |
3. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
П р я м о л и н е й н о е р а в н о м е р н о е д в и ж е н и е — это движение, при котором модуль и направление скорости не изменяются.
При прямолинейном равномерном движении вектор скорости постоянная величина: 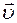 = const. Следовательно, при этом движении ускорение равно нулю.
= const. Следовательно, при этом движении ускорение равно нулю.
При прямолинейном равномерном движении средняя и мгновенная скорости равны между собой:
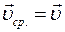 =
= 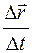 .
.
3.1. Формулы прямолинейного равномерного движения
При прямолинейном движении положение точки характеризует одна координата. Нарисуем ось координат ОХ, которая параллельна траектории движения точки (рис. 29):
х0 — это начальная координата (координата точки в начальный момент времени t 0),
х — это координата точки в момент времени t,
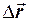 — это перемещение точки за интервал времени Δt = t - t0.
— это перемещение точки за интервал времени Δt = t - t0.
Из определения скорости находим формулу перемещения точки за интервал времени Δt
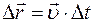 .
.
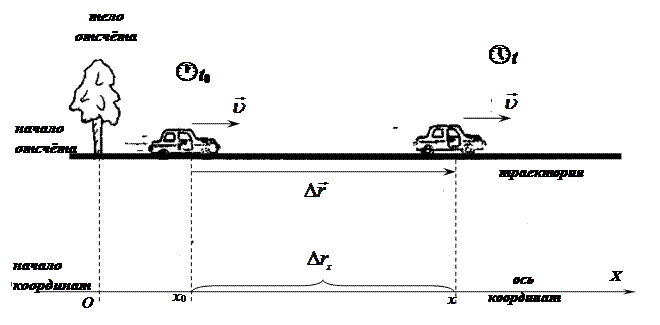
Рис. 29
В проекциях на ось координат ОХ получаем
Δrx = vx·Δt, или x - x0 = vx·Δt, откуда
х = х0 + vx· (t - t0) — это формула зависимости координаты
тела от времени t.
vx = 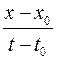 — это формула зависимости
— это формула зависимости
проекции скорости на ось ОХ от времени.
Так как Δr = S, получаем:
S = v·Δt — это формула пути.
 3.2. Графики прямолинейного равномерного движения
3.2. Графики прямолинейного равномерного движения
График зависимости проекции скорости от времени.
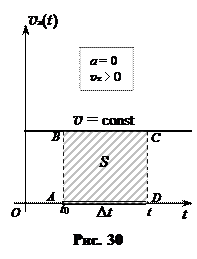
При прямолинейном равномерном движении скорость тела не изменяется. Поэтому график зависимости проекции скорости от времени — прямая линия, параллельная оси времени (рис. 30).
По графику зависимости проекции скорости от времени можно найти путь, пройденный телом за интервал времени Δt. Путь тела S за интервал времени Δt определяется площадью прямоугольника ABCD:
S = AB·AD = v·Δt.
График зависимости координаты точки от времени x = x(t).
 Из формулы зависимости координаты точки от времени х = х0 + vx× t (при t0 = 0) следует, что координата — линейная функция времени. Поэтому график х = x(t) — прямая линия, которая образует угол a с осью времени (рис. 31). По графику зависимости координаты точки от времени можно найти:
Из формулы зависимости координаты точки от времени х = х0 + vx× t (при t0 = 0) следует, что координата — линейная функция времени. Поэтому график х = x(t) — прямая линия, которая образует угол a с осью времени (рис. 31). По графику зависимости координаты точки от времени можно найти:
— координату точки в любой момент времени x(t),
— путь за любой интервал времени S =|Δrx | = |Δx|,
— проекцию скорости vx = 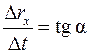 .
.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. При каком движении модуль мгновенной скорости равен модулю средней скорости?
2. Почему при прямолинейном равномерном движе- нии тангенциальное и нормальное ускорения равны нулю?
3. Какой вид имеет график зависимости скорости от времени для прямолинейного равномерного движения?
| график | graph | graphe | gráfica |
| зависимость | dependence | dépendence | dependencia |
| зависеть | depend | dépendre | depender |
| линейная функция | linear function | function linéaire | functión lineal |
| образовать | make | former | formar |
| угол | angle | un angle | un ángulo |
| таблица | table | table | tabla |
4. ПРЯМОЛИНЕЙНОЕ НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
При п р я м о л и н е й н о м н е р а в - н о м е р н о м д в и ж е н и и скорость тела изменяется по модулю, но не изменяется по направлению. При этом движении нормальное ускорение равно нулю: 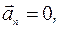 а тангенциальное ускорение не равно нулю
а тангенциальное ускорение не равно нулю 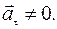 При прямолиней- ном неравномерном движении полное ускорение равно тангенциальному ускорению:
При прямолиней- ном неравномерном движении полное ускорение равно тангенциальному ускорению: 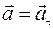 .
.
Мы будем изучать частный случай прямоли- нейного неравномерного движения — прямоли- нейное р а в н о п е р е м е н н о е движение.
4.1. Прямолинейное равнопеременное движение
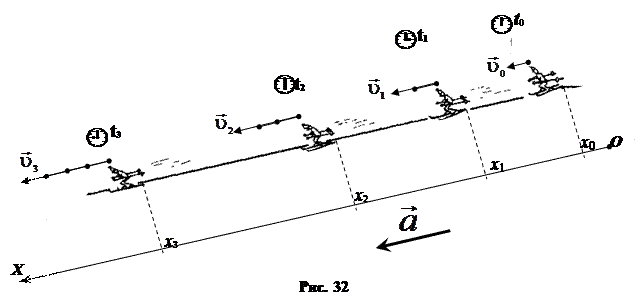 |
П р я м о л и н е й н о е р а в н о п е р е м е н н о е д в и ж е н и е — это движение, при котором скорость тела за любые равные интервалы времени изменяется на равную величину (рис. 32). Это значит, что если
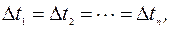 то
то 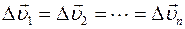 ,
,
тогда 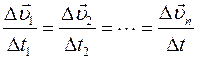 , или
, или
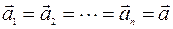 .
.
При прямолинейном равнопеременном движении ускорение не изменяется, т.е.
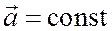 .
.
4.2. Основные формулы прямолинейного равнопеременного движения
|
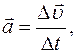 или
или 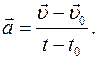 (Ⅰ.1)
(Ⅰ.1)
|
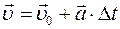 (Ⅰ.2)
(Ⅰ.2)
или в проекциях на ось ОХ
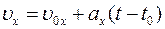 . (Ⅰ.3)
. (Ⅰ.3)
|
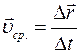 для любого
для любого
движения. При равнопеременном движении средняя скорость может быть вычислена по формуле
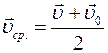 , (Ⅰ.4)
, (Ⅰ.4)
так как при равнопеременном движении скорость — линейная функция времени.
|
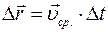
Подставим сюда формулу средней скорости (Ⅰ.4), а затем формулу мгновенной скорости (Ⅰ.2) 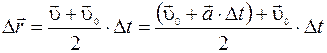 .
.
После вычислений получаем
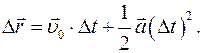 (Ⅰ.5)
(Ⅰ.5)
В проекциях на ось ОХ:
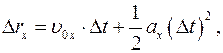
откуда находим формулу зависимости координаты точки
от времени
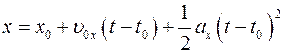 . (Ⅰ.6)
. (Ⅰ.6)
Из формул
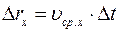 ,
,
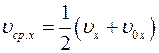 ,
,
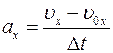
получаем еще одну формулу — формулу зависимости проекции перемещения от скорости тела:
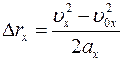 .
.
Равнопеременное движение может быть равноускоренным и равнозамедленным.
При р а в н о у с к о р е н н о м д в и ж е н и и модуль скорости увеличивается: v > v0, поэтому вектор скорости и вектор ускорения имеют одинаковые направления: 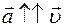 .
.
При р а в н о з а м е д л е н н о м д в и ж е н и и модуль вектора скорости уменьшается: v < v0, поэтому вектор скорости и вектор ускорения имеют противоположные направления: 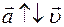 .
.
4.3. Графики равнопеременного движения
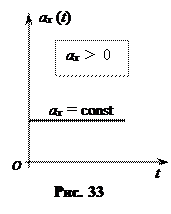 |
График зависимости ускорения от времени aх = aх(t)
При равнопеременном движении 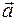 =const. Поэтому график ах = ах(t)— это прямая линия, параллельная оси времени (рис. 33).
=const. Поэтому график ах = ах(t)— это прямая линия, параллельная оси времени (рис. 33).
График зависимости проекции скорости от времени vх = vх (t).
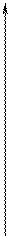
|
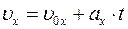 (при t0 = 0) следует, что скорость есть линейная функция времени. Поэтому график vх= vх (t) — это прямая линия, которая образует
(при t0 = 0) следует, что скорость есть линейная функция времени. Поэтому график vх= vх (t) — это прямая линия, которая образует

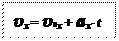 угол β с осью времени (рис. 34).
угол β с осью времени (рис. 34).


|
|




|
|
|
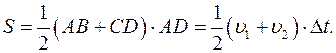
|




|
Из формулы координаты 
|
|
|
|
|
|
|
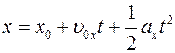
 (при t0 = 0) следует, что график x = x(t) — парабола (рис. 35).
(при t0 = 0) следует, что график x = x(t) — парабола (рис. 35).
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Почему при прямолинейном неравномерном движении ап = 0?
2. Почему при прямолинейном неравномерном
движении аτ ≠ 0?
3. Какой вид имеет график зависимости скорости от
времени для равнопеременного движения?
| движение равно- переменное | motion uniformly changing | mouvement uniformément varié | movimiento unifor- memente variado |
| движение равно- замедленное | motion uniformly retarded | mouvement uniformément retardé | movimiento unifor- memente retardado |
| движение равно- ускоренное | motion uniformly accelerated | mouvement uniformément accéléré | movimiento unifor- memente аcelerado |
4.4. Свободное падение
С в о б о д н о е п а д е н и е — это движение тела в пустоте из состояния покоя под действием притяжения тела к Земле.
Свободное падение — это прямолинейное равноускоренное движение. Все тела в данном месте Земли движутся при свободном падении с одинаковым ускорением. Это ускорение называется ускорением свободного падения и обозначается (буквой) “g”. Численное значение g » 9,8 м/с2. Вектор 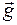 направлен вертикально вниз.
направлен вертикально вниз.
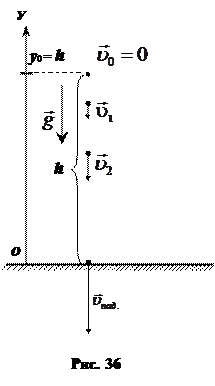 При свободном падении векторы ускорения и скорости имеют одинаковые направления
При свободном падении векторы ускорения и скорости имеют одинаковые направления 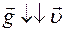 (рис. 36).
(рис. 36).
Формулы свободного падения мы получаем из формул прямолинейного равнопеременного движения. (См. 34) Считаем, что ось ОУ направлена вертикально вверх, начало координат выбираем на поверхности Земли.
Для свободного падения в этой системе координат:
начальная координата yo = h;
проекция начальной скорости v0y = 0;
проекция ускорения на ось ОУ ау = - g.
Уравнение зависимости проекции скорости vy от времени t (t0 = 0) имеет вид v y = - gt.
Уравнение зависимости координаты у от времени t t0 = 0) имеет вид 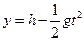 .
.
Откуда время падения тела с высоты h (у = 0) находим по формуле 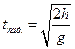
Формула зависимости проекции перемещения от скорости будет иметь вид
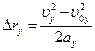 или
или 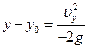 или
или 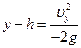
откуда модуль скорости падения тела с высоты h
(у = 0, у0 = h ) можно найти по формуле: 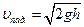
4.5. Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх,― это движение, при котором:
― начальная скорость тела направлена вертикально вверх,
― тело движется равнопеременно с постоянным ускорением 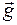 , направленным вертикально вниз.
, направленным вертикально вниз.
Это движение состоит из двух этапов: движения тела вертикально вверх и движения вертикально вниз.
При движении тела вертикально вверх модуль скорости уменьшается, поэтому вектор ускорения и вектор скорости имеют противоположные направления 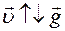 .Это равнозамедленное движение (рис. 37).
.Это равнозамедленное движение (рис. 37).
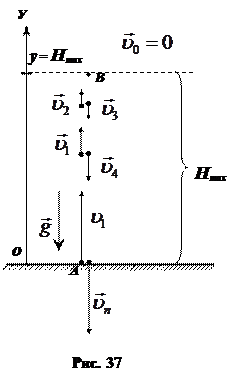 На максимальной высоте, равной Нmах, скорость тела становится равной нулю. После этого начинается второй этап движения — равноускоренное движение.
На максимальной высоте, равной Нmах, скорость тела становится равной нулю. После этого начинается второй этап движения — равноускоренное движение.
Можно доказать, что время подъёма тела на максимальную высоту Hmах равно времени падения с этой высоты до того уровня, с которого бросили тело:
Δtподъёма = Δtпадения
(Δt (от точки А до точки В ) = Δt (от точки В до точки А)).
Начальная скорость тела, брошенного вертикаль- но вверх, по модулю равна конечной скорости свободного падения
v0 = vп.
Формулы движения тела, брошенного вертикаль- но вверх, мы получаем из формул равнопеременного движения. Считаем, что ось ОУ направлена вертикально вверх, начало координат выбираем на поверхности Земли.
Для движения тела, брошенного вертикально вверх в этой системе координат (рис. 37):
начальная координата : у0 = 0;
проекция начальной скорости на ось ОУ: v0у = v0;
проекция ускорения на ось ОУ: ау= - g.
Уравнение зависимости проекции скорости vу от времени t (t0 = 0) имеет вид
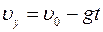 .
.
Уравнение зависимости координаты у от времени t при t0 = 0 имеет вид
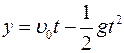 .
.
Зависимость модуля скорости v от координаты у
v02 - v 2 = 2g (у - y0).
Максимальная высота подъема тела у = Нmax, если у0 = 0
Нmax = 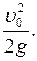
Скорость тела на максимальной высоте (h = Нmах)
v H = 0.
Время подъема тела на высоту Нmах
Δt подъёма = t H = 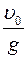 .
.
Полное время движения тела Δt движения = tп - t0
tп- t0 = 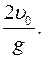
Время падения тела с высоты Нтах на Землю
tп - tH = 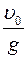 .
.
Модуль конечной скорости падения тела на Землю
v п = v0.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. Почему свободное падение — это равнопе- ременное движение?
2. Почему свободное падение — это равно- ускоренное движение?
3. Как изменяется скорость при подъёме?
4. Как изменяется скорость при падении?
| частный случай | special case | cas particulier | caso particular |
| свободное падение | free fall | chute libre | caida libre |
| падать | fall | tomber | caer |
| вертикально вниз | vertically downwards | verticalement vers le bas | hacia abajo |
| вертикально вверх | vertically upwards | verticalement vers le haut | hacia arriba |
| бросить | throw | lancer | lanzar |
| высота | height | hauteur | altura |
| этап | stage | étape | etapa |
Дата добавления: 2015-09-28; просмотров: 1200;

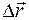 и координата х
и координата х