Абсолютное движение точки
Движение точки М относительно неподвижной системы координат называют абсолютным. Соответственно, траекторию (рис. 8.1), скорость и ускорение относительно неподвижной системы координат называют абсолютными.
Абсолютная скорость и абсолютное ускорение точки обозначается индексом а: 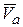 ,
, 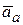 . Положение точки М относительно неподвижной системы координат O1x1y1z1 определяется радиус-вектором
. Положение точки М относительно неподвижной системы координат O1x1y1z1 определяется радиус-вектором 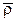 . Введем орты неподвижной системы координат
. Введем орты неподвижной системы координат 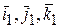 и разложим по ним радиус-вектор
и разложим по ним радиус-вектор 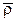 :
:
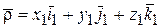 .
.
Тогда уравнения абсолютного движения точки имеют вид
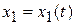 ,
, 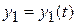 ,
, 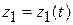 . (8.3)
. (8.3)
Исключив в уравнениях (8.3) время 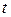 , получим уравнения траектории абсолютного движения точки (рис.8.1).
, получим уравнения траектории абсолютного движения точки (рис.8.1).
Чтобы найти скорость абсолютного движения точки, необходимо продифференцировать вектор-функцию 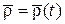 :
:
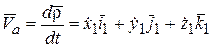 .
.
Раскладывая вектор 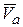 по ортам
по ортам
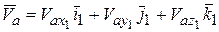
и, сравнивая обе записи вектора 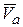 , получим
, получим
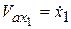 ,
, 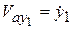 ,
, 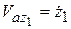 .
.
Аналогично, ускорение абсолютного движения точки равно:
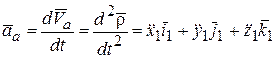 .
.
Раскладывая вектор 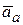 по ортам
по ортам
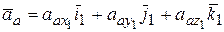 и сравнивая обе записи вектора
и сравнивая обе записи вектора 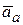 , получим
, получим
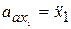 ,
, 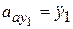 ,
, 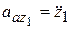 .
.
Дата добавления: 2015-09-21; просмотров: 2000;
