Относительное движение

Движение точки М относительно подвижной системы координат называют относительным. Соответственно, траектория (рис. 8.1), скорость и ускорение точки в ее движении относительно подвижной системы координат называются относительными. Относительная скорость и относительное ускорение точки обозначается индексом r: 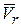, 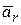. Положение точки М по отношению к системе координат Oxyz определяет радиус-вектор .

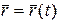Введем орты подвижной системы координат 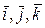и разложим радиус-вектор по ортам

.

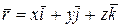Уравнения

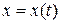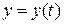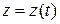, , (8.1)

являются уравнениями относительного движения точки в координатной форме. Движение самой координатной системы Oxyz не учитывается, считаем ее неподвижной.

Если в уравнениях (8.1) исключить время, то получим уравнения траектории относительного движения (рис. 8.1).

Если относительное движение задано, то для того, чтобы найти относительную скорость точки 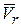, необходимо продифференцировать вектор-функцию 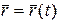в предположении, что орты 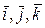неподвижны.

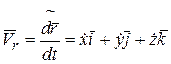. (8.1а)

Знак ~ (тильда) в равенстве (8.1а) означает, что производная берется в предположении, что 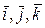- постоянные векторы. Такая производная называется локальной или относительной производной.

Раскладывая вектор 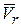по ортам

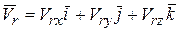
и сравнивая две записи вектора 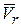, имеем

, , .

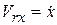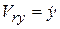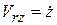Аналогично ускорение относительного движения точки равно:

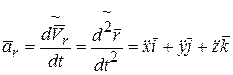. (8.2)

Раскладывая вектор 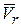по ортам

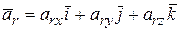
и сравнивая обе записи вектора 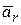, имеем

, , .

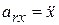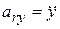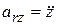Следовательно, для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.