Векторные формулы для скоростей и ускорений точек тела при вращательном движении

Скорость точки вращающегося твердого тела по модулю и направлению можно представить формулой Эйлера

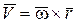, (7.13)

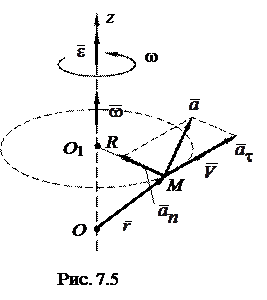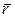где - радиус-вектор точки М, проведенный из произвольной точки оси вращения Oz, например, из точки О (рис.7.5).

Убедимся в справедливости этой формулы.

Вектор 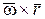перпендикулярен плоскости, в которой расположены векторы, входящие в векторное произведение. По направлению он параллелен вектору скорости 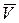, направленному по касательной к траектории (окружности) точки. Модуль векторного произведения равен

,

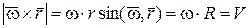т.к. .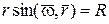

Таким образом, векторное произведение 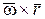по модулю и направлению определяет скорость точки при вращательном движении тела.

Ускорение точки по определению равно:

.

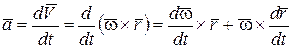Так как 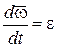, 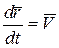получим

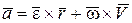. (7.14)

Вектор 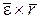направлен по касательной к траектории точки. По модулю он равен

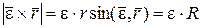
и следовательно эта составляющая ускорения является касательной составляющей ускорения точки М

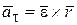. (7.15)

Ее называют также вращательным ускорением.

Вектор 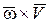направлен в плоскости окружности радиуса 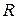от точки М к точке 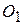. По модулю он равен

,

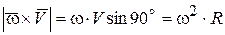и, следовательно, эта составляющая ускорения является нормальной составляющей ускорения точки М

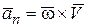. (7.16)

Ее называют также осестремительным ускорением.