Распределение скоростей и ускорений в теле при вращательном движении

Выберем в теле произвольную точку М. Обозначим ее начальное положение М₀. Проведем через нее и ось вращения неподвижную плоскость отсчета П_о. Свяжем также точку М с подвижной плоскостью П. Если закон вращательного движения задан 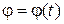, то положение точки М в момент времени t будет определяться углом 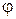. Траекторией точки М будет окружность, лежащая в плоскости перпендикулярной оси вращения. На рис. 7.1 изображено это сечение.

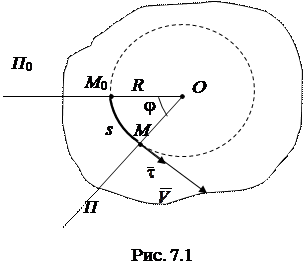
Пусть задано положительное направление отсчета угла 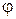против хода часовой стрелки в сторону движения. П₀, П – прямые пересечения соответствующие плоскостей с плоскостью сечения. Тогда зависимость дуги от угла запишется для движения точки М следующим образом

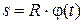, (7.5)

где 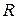- радиус окружности, по которой движется точка.

Так как 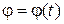задано, то таким образом движения точки М будет задано естественным способом. При этом проекция вектора скорости точки на касательную равна

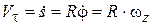. (7.6)

Направление вектора скорости точки определяется направлением вращения тела:

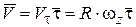. (7.7)

Таким образом, величина скорости 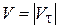равна:

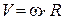. (7.8)

Скорости точек тела при его вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси. Скорости точек тела направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.

Определим ускорение произвольной точки М при естественном способе задания ее движения (7.5). Раскладывая ускорение точки на касательную и нормальную составляющие 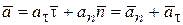, получим

,

.

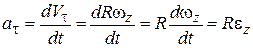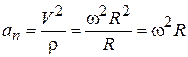Величина полного ускорения равна .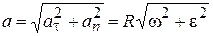

Таким образом, ускорение произвольной точки тела при вращательном движении вокруг неподвижной оси определяется по формулам:

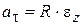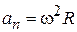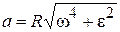, , . (7.9)

Как видно из формул (7.9) касательное, нормальное и полное ускорения точек, как и скорости, распределены по линейному закону. Они линейно зависят от расстояний до оси вращения. Вектор нормального ускорения направлен по радиусу окружности к оси вращения (рис.7.2).

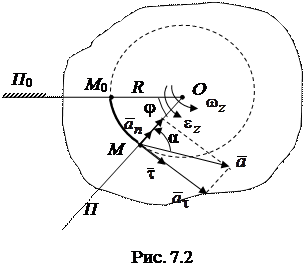
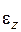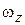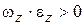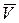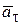Направление вектора касательного ускорения зависит от знака алгебраического углового ускорения. Если знаки и совпадают, т.е. , то направления векторов и совпадают, если 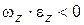, то векторы 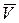и 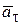направлены противоположно друг другу.

Обозначим угол α между полным ускорением 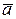и радиусом вращения. Имеем

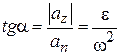, (7.10)

т.е. угол α для всех точек тела один и тот же и от расстояния до оси вращения не зависит. Откладывать его следует от вектора ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения, независимо от направления вращения тела.