Теорема сложения ускорений при переносном поступательном движении

Абсолютное ускорение точки, совершающей сложное движение при переносном поступательном движении равно геометрической сумме относительного и переносного ускорения:

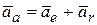. (8.9)

Доказательство:

Вернемся к рис. 8.1. При переносном поступательном движении орты 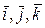не меняются не только по величине, но и по направлению, т.е. это постоянные векторы, а т.к. производные от постоянных векторов, а т.к. производные от постоянных векторов равны нулю, то по формуле (8.6)

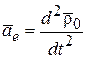. (8.10)

Для определения абсолютного ускорения точки продифференцируем дважды радиус-вектор 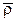(8.4) по времени, учитывая постоянство ортов :

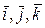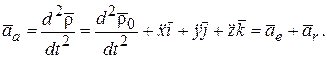
В последнем выражении первое слагаемое по формуле (8.10) представляет переносное ускорение 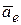, а последние три по формуле (8.2) – относительное ускорение 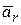. Теорема доказана.

Теорема сложения ускорений при произвольном переносном движении (теорема Кориолиса)

Абсолютное ускорение точки 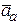определяется по теореме Кориолиса, согласно которой абсолютное ускорение точки, совершающей сложное движение, равно геометрической сумме переносного, относительно и кориолисова ускорений:

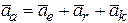. (8.11)

Кориолисово ускорение вычисляется по формуле:

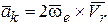, (8.12)

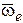где - вектор угловой скорости переносного движения, 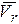- вектор относительной скорости точки. Направление вектора кориолисова ускорения определяется по правилу векторного произведения: кориолисово ускорение будет направлено перпендикулярно плоскости, в которой лежат векторы 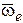и 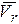(рис. 8.2), в ту сторону, откуда кратчайший поворот от вектора 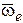к вектору 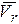видится происходящим против хода часовой стрелки.

Модуль кориолисова ускорения равен .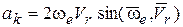

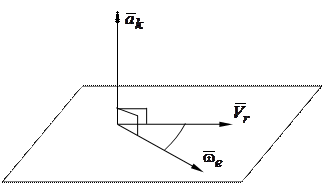
Рис. 8.2

Докажем справедливость теоремы для переносного вращательного движения.

Рис. 8.3

Пусть подвижная система координат Oxyz вращается вокруг оси l с угловой скоростью 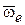(рис. 8.3). Во все время движения радиус-векторы точки по-прежнему связаны зависимостью

.

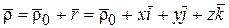Так как по определению 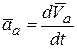, продифференцируем выражение (8.8) по времени, учитывая свойства производной вектора по скалярному аргументу:

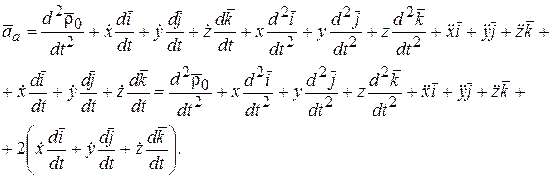
В последнем выражении первые четыре слагаемые представляют переносное ускорение 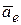, следующие три слагаемые представляют относительную скорость 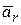. Оставшиеся слагаемые обозначим (*). В выражении (*) производная от каждого орта по времени представляет собой линейную скорость точки, для которой этот орт является радиусом-вектором. Например для орта 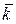(рис. 8.3) скорость 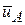точки А его конца равна

.

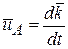Но так как орт 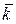вращается вокруг оси l, то скорость его конца можно определить по векторной формуле Эйлера:

.

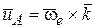Следовательно

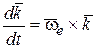. (8.14)

Аналогично для ортов 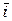и :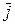

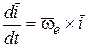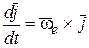, . (8.15)

Подставляя формулы (8.14) и (8.15) в выражение (*), получим

(*)= .

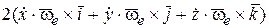Используя сочетательное свойство векторного произведения относительно числовых множителей, какими являются 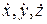, имеем

(*)= .

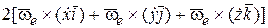Далее, используя распределительное свойство для векторного произведения, получим

(*)= .

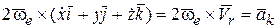Таким образом,

.

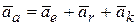Теорема для переносного вращательного движения доказана.