Мгновенный центр скоростей

Формула (9.4) существенно упрощается, если в качестве полюса выбрать в рассматриваемый момент времени такую точку подвижной плоскости 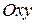жестко связанной с плоской фигурой, скорость которой равна нулю. Такая точка носит название мгновенного центра скоростей. Обозначим ее – Р. Точка Р не обязательно принадлежит плоской фигуре. Она принадлежит подвижной плоскости .

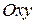Теорема: Если в некоторый момент времени плоское движение тела таково, что 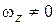, то

1. Мгновенный центр скоростей существует и он единственный.

2. Распределение скоростей в данный момент времени таково, как если бы тело совершало вращательное движение вокруг оси, проходящей через мгновенный центр скоростей.

Доказательство:

Пусть для определенности 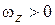и существует точка А, скорость которой не равна нулю в заданный момент времени 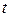(иначе точка А – мгновенный центр скоростей) (рис. 9.8). Повернем вектор 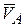на 90° в направлении дуговой стрелки 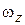( 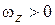) и отложим на этом луче отрезок

.

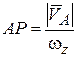Так как 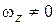, то АР – конечное число. Возьмем точку А в качестве полюса и вычислим скорость точки Р по формуле (13.4): ,

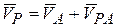где .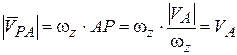

А так как 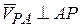, то .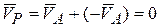

Итак, 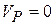и точка Р – мгновенный центр скоростей. Из построения видно, что эта точка единственная.

2. Примем точку Р за полюс. Тогда

формула (9.4) будет иметь вид

.

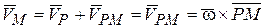Следовательно, .

Теорема доказана.