Распределение скоростей при плоском движении

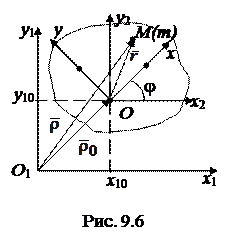Вернемся к рис. 9.4. Определим скорость произвольной точки М плоской фигуры относительно осей 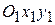в заданный момент времени.

Введем векторы 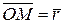, , 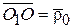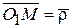(рис. 9.6). Очевидно, что .

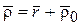Рассмотрим движение точки М как сложное, состоящее из переносного поступательного движения плоской фигуры вместе с осями 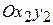и относительного движения точки, которое будет происходить так, как двигаются точки тела, вращающегося вокруг оси 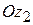, направленной перпендикулярной плоскости рисунка на читателя. Тогда скорость точки М относительно неподвижной системы координат 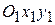является абсолютной скоростью и определяется по теореме сложения скоростей

.

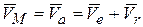Пусть (m) – точка подвижной плоскости 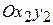, с которой совпадает в заданный момент времени точка плоской фигуры М. Тогда, так как переносное движение поступательное, то

.

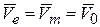Относительная скорость точки от вращательного движения плоской фигуры вокруг оси 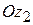( или относительно полюса О) по формуле Эйлера равна 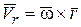и следовательно,

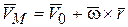или

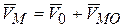. (9.4)

В формуле (9.4) символическая запись 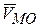означает «скорость точки М от вращательного движения вокруг точки О».

Таким образом, скорость произвольной точки плоской фигуры в некоторый момент времени равна геометрической сумме скорости полюса и скорости рассматриваемой точки в относительном вращательном движении плоской фигуры вокруг полюса.

Покажем, как найти скорость точки тела в заданный момент времени по формуле (9.4), если задан закон плоского движения:

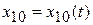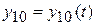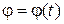, , . (9.5)

По первым формулам (9.5), определяющим закон движения полюса О, определим вектор 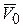по величине и направлению (рис. 9.7). По третьей формуле (9.5) определим угловую скорость плоской фигуры 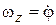. Пусть вращение происходит по часовой стрелке. По модулю 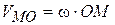. Направим вектор 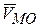перпендикулярно ОМ в сторону вращения плоской фигуры. Вектор скорости точки М получим, сложив векторы 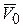и 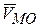по правилу параллелограмма.