Разложение плоского движения твердого тела на два простых движения – поступательное и вращательное

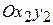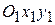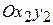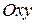Вернемся к рис. 9.4 и введем вспомогательную подвижную систему координат , совершающую поступательное движение относительно системы координат . При поступательном движении осей оси будут совершать по отношению к ним вращательное движение вокруг полюса. Как известно для задания поступательного движения тела достаточно задать движения одной его точки, т.е. движение полюса О определяет поступательное движение осей :

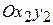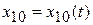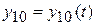, . (9.2)

Примем это движение за переносное. Тогда вращательное движение осей 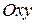относительно подвижных осей 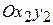, определяемое уравнением

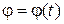(9.3)

будет относительным.

От выбора полюса О вид функции (9.3) зависит существенным образом, а вид функции (9.3) от выбора точки О не зависит. Покажем это.

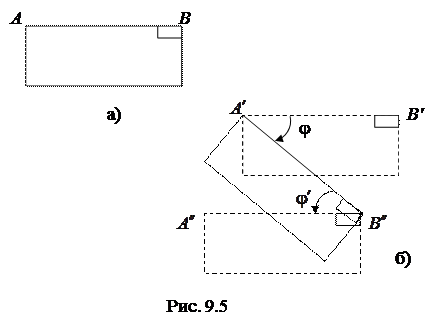
Возьмем для наглядности прямоугольную фигуру. На рис 9.5 изображено начальное положение фигуры а) прямоугольника АВ и конечное положение б). Выберем сначала за полюс точку А и переместим прямоугольник АВ из положения а) в положение В сначала параллельным переносом (положение 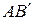), а затем поворотом вокруг полюса А на угол j. Затем выберем за полюс точку В и переместим прямоугольник АВ из положения а) в положение б) параллельным переносом в положение 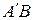, затем поворотом вокруг полюса В на угол 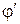. Из рисунка видно, что по величине 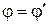и откладываем угол в обоих случаях в одном направлении – по ходу часовой стрелки.

Вывод: Введением вспомогательной системы координат 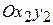плоское движение оказывается разложенным на два следующих движение: переносное – поступательное движение вместе с вспомогательной системой координат (определяется движением полюса) и относительное – вращательное движение подвижной плоскости 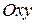вместе с плоской фигурой вокруг полюса (определяется углом поворота j).

При этом, поскольку выбор полюса произволен, то указанное разложение может быть выполнено бесчисленным множеством способов. Однако, во всех таких разложениях относительное вращательное движение остается одним и тем же, так как уравнение 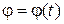от выбора полюса не зависят.