Способы отыскания мгновенного центра скоростей
Рассмотрим некоторые частные случаи. На рис. 9.8 - 9.10 показаны способы нахождения мгновенного центра скоростей по скоростям двух точек плоскости фигуры. На рис. 9.8 известен вектор скорости 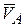 , точки А и прямая, по которой направлен вектор скорости точки В.
, точки А и прямая, по которой направлен вектор скорости точки В.

Мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям, восстановленным в этих точках. Угловая скорость ω находится по известной величине скорости 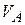 :
: 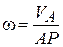 .
.
В случае, показанном на рис. 9.9 угловую скорость можно найти, пользуясь свойством пропорции, по одной из формул:
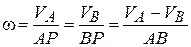 .
.

В случае, показанном на рис. 9.10, угловую скорость можно определить по формулам:
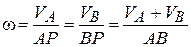 .
.
В случае, когда скорости точек А и В плоской фигуры параллельны, но не перпендикулярны к АВ (рис. 9.11), мгновенный центр скоростей находится в бесконечности и, следовательно, угловая скорость равна нулю. Векторы скоростей всех точек плоской фигуры в данный момент времени будут равны:
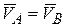 .
.
Движение плоской фигуры в этом случае в данный момент времени называют мгновенно поступательным.
 При качении без скольжения одного цилиндрического тела по поверхности другого (рис. 9.12) мгновенный центр скоростей совпадает с точкой соприкосновения тле, так как при отсутствии скольжения
При качении без скольжения одного цилиндрического тела по поверхности другого (рис. 9.12) мгновенный центр скоростей совпадает с точкой соприкосновения тле, так как при отсутствии скольжения 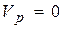 . Угловую скорость тела в этом случае можно вычислить по формуле
. Угловую скорость тела в этом случае можно вычислить по формуле
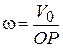 .
.
Дата добавления: 2015-09-21; просмотров: 834;
