Векторный и скалярный потенциалы электромагнитного поля
Непосредственное решение системы уравнений Максвелла, как правило, весьма сложно, поскольку здесь определению подлежат шесть неизвестных составляющих векторов 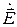 и
и 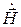 . Поэтому бывает целесообразным найти некоторую вспомогательную функцию, знание которой позволило бы одновременно найти векторы напряженности электрического и магнитного полей. Подобные вспомогательные функции в электродинамике носят название потенциалов электромагнитного поля.
. Поэтому бывает целесообразным найти некоторую вспомогательную функцию, знание которой позволило бы одновременно найти векторы напряженности электрического и магнитного полей. Подобные вспомогательные функции в электродинамике носят название потенциалов электромагнитного поля.
Отметим, прежде всего, что третьему уравнению Максвелла удовлетворяет векторное поле 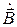 , определяемое по формуле
, определяемое по формуле
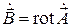
Здесь 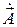 — некоторая векторная функция, носящая название электрического векторного потенциала. Подобное название обусловлено тем, что эта величина естественно используется в тех задачах, которые связаны с возбуждением электромагнитного поля электрическими сторонними токами. Аналогично
— некоторая векторная функция, носящая название электрического векторного потенциала. Подобное название обусловлено тем, что эта величина естественно используется в тех задачах, которые связаны с возбуждением электромагнитного поля электрическими сторонними токами. Аналогично
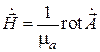 .
.
Последние два соотношения весьма неопределенны, поскольку единственное условие, налагаемое на 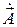 , — это дифференцируемость, обеспечивающая существование ротора данного векторного поля.
, — это дифференцируемость, обеспечивающая существование ротора данного векторного поля.
Попытаемся при помощи электрического векторного потенциала определить вектор напряженности электрического поля, для этого подставим выражение векторного потенциала во второе уравнение Максвелла:
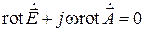 ,
,
т. е.
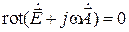 .
.
В силу известного тождества векторного анализа
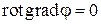
вышеприведенное соотношение будет выполняться автоматически, если
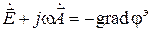
Здесь 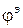 — некоторая скалярная функция, называемая скалярным электрическим потенциалом.
— некоторая скалярная функция, называемая скалярным электрическим потенциалом.
Выбор знака в правой части последней формулы обусловлен тем, что в соответствии с известным соотношением электростатики для полей, не зависящих от времени, справедливо равенство
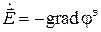
При этом сохраняется традиционное направление стрелок на силовых линиях электрического поля, при котором истоком поля считается положительный заряд.
Итак, в данном разделе найден способ выражения векторов электромагнитного поля через векторный и скалярный электрические потенциалы:
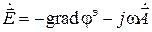 ,
,
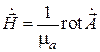
Дата добавления: 2015-10-19; просмотров: 1411;
