Векторный способ задания движения точки. Аксиомы классической кинематики

Аксиомы классической кинематики

Кинематика– базируется на аксиомах классической евклидовой геометрии, аксиомах о равномерном течении времени и непрерывности движения.

Кинематика точки

Способы задания движения точки

В кинематике как хроногеометрии движение точки должно быть задано.

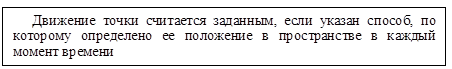
Известны три способа задания движения точки: векторный, координатный и естественный.

Векторный способ задания движения точки

Векторный способ задания движения вытекает из физических основ механики. Он связан с измерением отрезков и углов (направлений).
В силу этого этот способ практически не применяется в ТМ для решения задач. В курсе ТМ к нему обращаются в основном для определения кинематических мер, для записи формул и т. д.

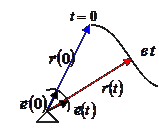
При векторном (физическом) способе задания движения точки ей ставится в соответствие в каждый момент времени ее радиус-вектор относительно некоторого условного неподвижного центра – полюса. Таким образом, радиус-вектор (рис. 1) является непрерывной векторной функцией аргумента t:

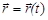. (1)

Это означает, что в каждый момент движения точки задаются как величина r = r(t), так и направлени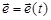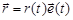е : , где .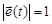

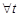Зависимость 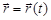задает закон движения точки.

У свободно движущейся точки число кинематически независимых движений равно 3: по осям xyz. В связи с этим говорят о 3 степенях свободы (s) движения точки.

s = 1_x + 1_y + 1_z = 3.

Таким образом, движение точки происходит в 3-мерном пространстве ее движений, совпадающем по размерности с 3-мерным пространством вещественных материальных форм, называемом в современной науке просто пространством.