Вычисление скорости точки в естественных осях
Вычислим скорость точки в естественных осях на основе (14) и определения (15). Тогда с учетом того, что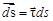 
, получим
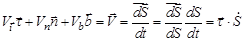(19)
, 
.
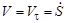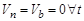Таким образом, скорость точки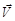 
всегда касательна к ее траектории.
3.1.4. Теорема о производной от единичного вектора
по параметру
Докажем важную для дальнейшего изложения материала вспомогательную теорему о производной от единичного вектора по параметру. Покажем, что она ортогональнасамому вектору.
Доказательство: пусть есть единичный вектор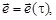 
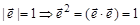. Вычислим производную: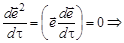 
^ 
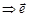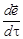, так как cosa = p/2. Что и следовало доказать.
Дата добавления: 2015-09-28; просмотров: 671;