Естественный способ задания движения точки. При естественном способе от точки-полюса вдоль траектории откладывается дуговая координата S

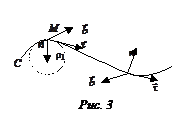 При естественном способе от точки-полюса вдоль траектории откладывается дуговая координата S. Условно выбирается положительное направление движения. Вводится связанный с движущейся точкой локальный декартов репер {
При естественном способе от точки-полюса вдоль траектории откладывается дуговая координата S. Условно выбирается положительное направление движения. Вводится связанный с движущейся точкой локальный декартов репер { 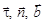 } – естественный трехгранник. Здесь
} – естественный трехгранник. Здесь
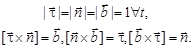
Касательный к траектории единичный вектор 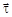 , задающий положительное направление движения точки, называется вектором тангенциали. Связанная с ним ось – тангенциальной или же тангенциалью.
, задающий положительное направление движения точки, называется вектором тангенциали. Связанная с ним ось – тангенциальной или же тангенциалью.
Вектор нормали 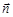 , перпендикулярный
, перпендикулярный 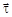 , всегда направлен на центр окружности кривизны, касательной к траектории в данной точке.
, всегда направлен на центр окружности кривизны, касательной к траектории в данной точке.
Вектор бинормали 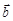 перпендикулярен к векторам
перпендикулярен к векторам 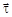 и
и 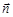 . Соответствующие им оси носят название нормали и бинормали.
. Соответствующие им оси носят название нормали и бинормали.
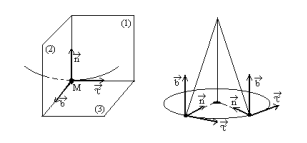
Рис. 4
Согласно рис. 4 векторы 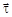 и
и 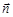 задают касательную или соприкасающуюся плоскость (1), в которой лежит окружность кривизны, касательная к траектории в данной точке. Векторы
задают касательную или соприкасающуюся плоскость (1), в которой лежит окружность кривизны, касательная к траектории в данной точке. Векторы 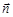 и
и 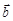 задают нормальную плоскость (2), а векторы
задают нормальную плоскость (2), а векторы 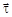 и
и 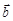 — спрямляющую плоскость (3). Полученный трехгранник, составленный из касательной, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Следует заметить, что окружности кривизны, касательные к траектории в различных ее точках, – разные. Причем каждая имеет свой радиус кривизны
— спрямляющую плоскость (3). Полученный трехгранник, составленный из касательной, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Следует заметить, что окружности кривизны, касательные к траектории в различных ее точках, – разные. Причем каждая имеет свой радиус кривизны 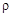 (рис. 5). При этом кривизну (к) как меру определяют по формуле
(рис. 5). При этом кривизну (к) как меру определяют по формуле
к = 1/r (13)
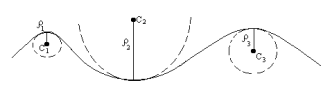
Рис. 5
Таким образом, например, кривизна прямой линии будет равна
к = 1/¥ ® 0, а кривизна точки к = 1/0®¥.
Как задается движение точки при естественном способе?
Здесь движение считается заданным, если явно задана зависимость
S = S(t). (14)
При этом предполагается, что векторы 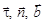 зависят неявно от времени. Это означает, что их производные по параметру t в общем случае отличны от нуля. Зависимость (14) задает закон движения точки. Например, так:
зависят неявно от времени. Это означает, что их производные по параметру t в общем случае отличны от нуля. Зависимость (14) задает закон движения точки. Например, так:
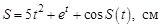
Дата добавления: 2015-09-28; просмотров: 901;
