Вычисление ускорения точки в естественных осях
Выведем формулу для вычисления ускорения точки в естественных осях на основе определения (16) и формулы (19). Согласно рис. 6
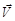 изменяется по величине и по направлению,
изменяется по величине и по направлению, 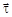 изменяется только по направлению:
изменяется только по направлению:
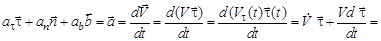
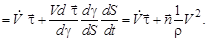 (20)
(20)
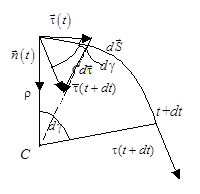
Рис. 6
В этом случае вычисление производной 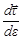 осуществим на основе рис. 6.
осуществим на основе рис. 6.
Изобразим элемент траектории точки dS с единичными векторами 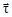 в моменты t и t + dt. Здесь
в моменты t и t + dt. Здесь 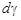 – угол смежности. Перенесем вектор
– угол смежности. Перенесем вектор 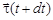 параллельно к моменту t. Так как векторы
параллельно к моменту t. Так как векторы 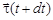 и
и 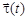 единичные, то, соединив их концы, получим:
единичные, то, соединив их концы, получим:
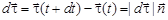 ,
,
где 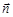 – центр окружности кривизны.
– центр окружности кривизны.
Так как 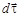 зависит от
зависит от 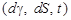 , то
, то
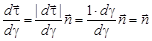 ,
,
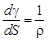 (так как
(так как 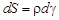 , где
, где 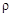 – радиус окружности кривизны).
– радиус окружности кривизны).
Таким образом,
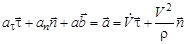 (21)
(21)
и вектор ускорения точки всегда лежит в касательной плоскости и раскладывается на тангенциальное и нормальное направления:
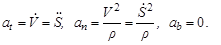
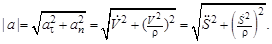 (22)
(22)
3.1.6. Определение радиуса кривизны траектории
через декартовы компоненты скорости и ускорения
Рассмотрим, как вычисляется радиус кривизны 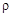 траектории в том случае, когда движение точки задано в декартовых координатах.
траектории в том случае, когда движение точки задано в декартовых координатах.
Запишем
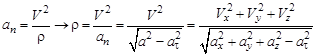 , (23)
, (23)
где 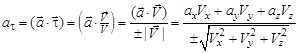
Дата добавления: 2015-09-28; просмотров: 637;
