Угловые скорость и ускорение как кинематические меры вращения твердого тела как целого

Из физических основ механики следует, что

4.3.2. Вычисление скоростей и ускорений точек тела
при его вращении вокруг неподвижной оси

Рис. 8

Так как при вращении твердого тела вокруг неподвижной оси траектория движения любой точки известна – это окружность (рис. 8), то кинематику такого движения целесообразно описывать в естественной системе координат.

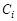– центр;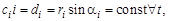

.

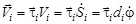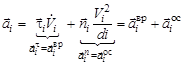, (28)

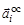где – вращательное ускорение; – осестремительное (центростремительное) ускорение.

Анализ выражений (28) показывает, что их можно представить как векторные произведения, если ввестив этом случае понятия угловой скорости и углового ускорения, как (26), (27).

Тогда

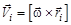; (29)

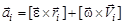. (30)

Выражения (29) называют формулой Эйлера, а (30) – формулой Ривальса.

Вычислим ускорение точки непосредственно по определению (16) и (29). Тогда

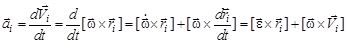, (31)

что тождественно (30).

Введя общепринятые в России обозначения

, ,

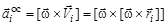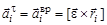получим, что

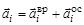. (32)