Цилиндрическая система координат

Цилиндрическая система координат (рис. 2) задается ортами 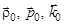, единичной длины 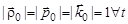, которые поворачиваются при движении точки, т. е. являются функциями времени: 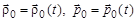. При этом

.

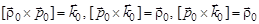Вектор 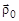задает полярно-радиальное направление (ось), а вектор 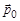– трансверсальное направление (ось), вектор 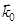во времени не изменяется и задает аксиальное направление (ось). Положение точки в пространстве определяется координатами: r – полярным радиусом,
j – полярным углом, z – координатой, аналогичной декартовой z.

Движение точки в цилиндрической системе координат считается заданным, если известны функции

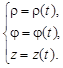(4)

Выражение (4) задает закон движения в цилиндрических координатах.

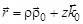. (5)

Если же движение точки происходит на плоскости, то говорят о полярной системе координат. При этом

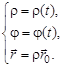(6)

2.3.4. Определение траектории точки
при координатном способе задания ее движения

Легко понять, что закон движения точек (3) или (4) задает траекторию параметрически, где в качестве параметра выступает время t. Поэтому траектория движущейся точки может быть построена по циклическому алгоритму:

1) задаем значение t = t₁;

2) вычисляем значение x, y, z или r, j, z по формулам (3) или (4);

3) возвращаемся к пункту 1);

4) и так до t = t_n.

Кроме того, уравнение траектории или уравнения траекторий могут быть получены аналитически. Для этого необходимо исключить параметр t из выражений системы (3).

В результате получится зависимость типа

F(x, y, z) = c,(7)

или F₁(x, y) = c₁, F₂(x, z) = c₂, F₃(y, z) = c₃.

Аналогично получим и для системы (4).

Рассмотрим пример. Пусть

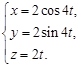(8)

Тогда в проекции на плоскость X0Y получим

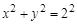. (9)

В проекции на X0Z:

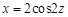. (10)

А в проекции на плоскость (Y0Z):

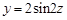. (11)

Совокупность уравнений (8)–(11) задает траекторию точки, которая является цилиндрической спиралью с шагом h = p (м).

Рассмотрим другой пример. Пусть

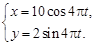
Тогда

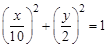. (12)

Уравнение (12) есть уравнение эллипса с полуосями 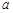= 10 м, b = 2 м. При любом другом законе движения поступаем аналогично.